Trong không gian với hệ trục tọa độ \(Oxyz\), cho hai vectơ \(\vec a\left( { - 1;0;3} \right)\)và \(\vec b\left( {1;2; - 1} \right)\). Tọa độ của vectơ \(\vec c = \vec a - \vec b\) là

Chọn hệ trục toạ độ \(Oxyz\) với gốc \(O\) đặt tại điểm xuất phát của hai khinh khí cầu, mặt phẳng \(\left( {Oxy} \right)\) trùng với mặt đất với trục \(Ox\) hướng về phía nam, trục \(Oy\) hướng về phía đông và trục \({\rm{Oz}}\) hướng thẳng đứng lên trời (tham khảo hình vẽ), đơn vị đo lấy theo kilômét.

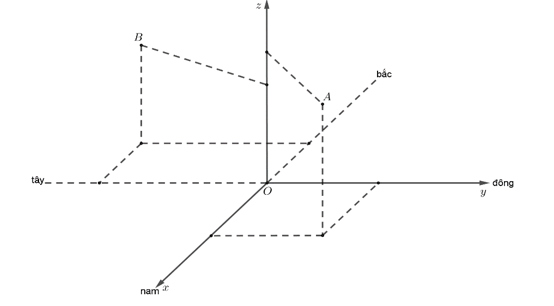
Chiếc khinh khí cầu thứ nhất và thứ hai ở vị trí \(A,B\). Ta có \(A\left( {\frac{5}{2};2;\frac{4}{5}} \right),B\left( { - \frac{3}{2}; - 3;\frac{3}{5}} \right)\).

Gọi \(C\) là điểm đối xứng của \(A\) qua mặt phẳng \(\left( {Oxy} \right)\), \(C\left( {\frac{5}{2};2; - \frac{4}{5}} \right)\).

Khi đó \(I = BC \cap \left( {Oxy} \right)\).

\(\overrightarrow {BC} = \left( {4;5; - \frac{7}{5}} \right)\). \(I \in \left( {Oxy} \right) \Rightarrow I\left( {x;y;0} \right) \Rightarrow \overrightarrow {BI} = \left( {x + \frac{3}{2};y + 3; - \frac{3}{5}} \right)\)

\(\overrightarrow {BC} ,\overrightarrow {BI} \) cùng phương nên \(\frac{{x + \frac{3}{2}}}{4} = \frac{{y + 3}}{5} = \frac{3}{7} \Rightarrow \left\{ \begin{array}{l}x = \frac{3}{{14}}\\y = - \frac{6}{7}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = \frac{3}{{14}}\\b = \frac{6}{7}\end{array} \right. \Rightarrow 2a + 3b = 3\).

Hàm số xác định và liên tục trên \(D = \left( { - \infty ;0} \right] \cup \left[ {1; + \infty } \right)\). Ta có:

\(a = \mathop {\lim }\limits_{x \to + \infty } \frac{{f\left( x \right)}}{x} = \mathop {\lim }\limits_{x \to + \infty } \frac{{2x - \sqrt {{x^2} - x} }}{x} = \mathop {\lim }\limits_{x \to + \infty } \left( {2 - \sqrt {1 - \frac{1}{x}} } \right) = 1\).

\(b = \mathop {\lim }\limits_{x \to + \infty } \left( {f\left( x \right) - x} \right) = \mathop {\lim }\limits_{x \to + \infty } \left( {x - \sqrt {{x^2} - x} } \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{x}{{x + \sqrt {{x^2} - x} }} = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{1 + \sqrt {1 - \frac{1}{x}} }} = \frac{1}{2}\).

\( \Rightarrow y = x + \frac{1}{2}\) là tiệm cận xiên của đồ thị hàm số khi \(x \to + \infty \).

\(a = \mathop {\lim }\limits_{x \to - \infty } \frac{{f\left( x \right)}}{x} = \mathop {\lim }\limits_{x \to - \infty } \frac{{2x - \sqrt {{x^2} - x} }}{x} = \mathop {\lim }\limits_{x \to - \infty } \left( {2 + \sqrt {1 - \frac{1}{x}} } \right) = 3\).

\(b = \mathop {\lim }\limits_{x \to - \infty } \left( {f\left( x \right) - 3x} \right) = - \mathop {\lim }\limits_{x \to - \infty } \left( {x + \sqrt {{x^2} - x} } \right) = - \mathop {\lim }\limits_{x \to - \infty } \frac{x}{{x - \sqrt {{x^2} - x} }} = - \mathop {\lim }\limits_{x \to - \infty } \frac{1}{{1 + \sqrt {1 - \frac{1}{x}} }} = - \frac{1}{2}\).

\( \Rightarrow y = 3x - \frac{1}{2}\) là tiệm cận xiên của đồ thị hàm số khi \(x \to - \infty \).

Vậy đồ thị hàm số có 2 đường tiệm cận xiên.