Câu hỏi:
12/12/2024 984
Thống kê chiều cao của tổ 1 và tổ 2 của lớp 10A cho bởi bảng sau:
Chiều cao (cm)
\(\left[ {150;155} \right)\)
\(\left[ {155;160} \right)\)
\(\left[ {160;165} \right)\)
\(\left[ {165;170} \right)\)
\(\left[ {170;175} \right)\)
\(\left[ {175;180} \right)\)
Số học sinh tổ 1
3
2
2
1
3
0
Số học sinh tổ 2
1
3
3
2
1
1
a) Tứ phân vị thứ nhất của mẫu số liệu về chiều cao của học sinh tổ 1 là \({Q_1} = 154,375\).
b) Khoảng biến thiên của mẫu số liệu về chiều cao của học sinh tổ 1 là \(R = 25\).
c) Phương sai của mẫu số liệu về chiều cao của học sinh tổ 2 là \(s_2^2 \approx 48,88\).
d) Độ lệch chuẩn của mẫu số liệu về chiều cao của học sinh tổ 2 lớn hơn độ lệch chuẩn của mẫu số liệu về chiều cao của học sinh tổ 1.
Thống kê chiều cao của tổ 1 và tổ 2 của lớp 10A cho bởi bảng sau:
|
Chiều cao (cm) |
\(\left[ {150;155} \right)\) |
\(\left[ {155;160} \right)\) |
\(\left[ {160;165} \right)\) |
\(\left[ {165;170} \right)\) |
\(\left[ {170;175} \right)\) |
\(\left[ {175;180} \right)\) |
|
Số học sinh tổ 1 |
3 |
2 |
2 |
1 |
3 |
0 |
|
Số học sinh tổ 2 |
1 |
3 |
3 |
2 |
1 |
1 |
a) Tứ phân vị thứ nhất của mẫu số liệu về chiều cao của học sinh tổ 1 là \({Q_1} = 154,375\).
b) Khoảng biến thiên của mẫu số liệu về chiều cao của học sinh tổ 1 là \(R = 25\).
c) Phương sai của mẫu số liệu về chiều cao của học sinh tổ 2 là \(s_2^2 \approx 48,88\).
d) Độ lệch chuẩn của mẫu số liệu về chiều cao của học sinh tổ 2 lớn hơn độ lệch chuẩn của mẫu số liệu về chiều cao của học sinh tổ 1.
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) S, b) Đ, c) Đ, d) S
a) Xét mẫu số liệu về chiều cao của học sinh tổ 1:
Cỡ mẫu \(n = 3 + 2 + 2 + 1 + 3 = 11\).
Tứ phân vị thứ nhất của mẫu số liệu là \({x_3}\) nên nhóm chứa tứ phân vị thứ nhất là \(\left[ {150;155} \right)\) và ta có \({Q_1} = 150 + \frac{{\frac{{11}}{4} - 0}}{3} \cdot 5 \approx 154,92\).
b) Khoảng biến thiên của mẫu số liệu về chiều cao của học sinh tổ 1 là \(R = 175 - 150 = 25\).
c) Xét mẫu số liệu về chiều cao của học sinh tổ 2:
\(\overline {{x_2}} = \frac{{1 \cdot 152,5 + 3 \cdot 157,5 + 3 \cdot 162,5 + 2 \cdot 167,5 + 1 \cdot 172,5 + 1 \cdot 177,5}}{{11}} \approx 163,41\).
\(s_2^2 = \frac{{1 \cdot 152,{5^2} + 3 \cdot 157,{5^2} + 3 \cdot 162,{5^2} + 2 \cdot 167,{5^2} + 1 \cdot 172,{5^2} + 1 \cdot 177,{5^2}}}{{11}} - 163,{41^2} \approx 48,88\).
d) Độ lệch chuẩn của mẫu số liệu về chiều cao của học sinh tổ 2 là \({s_2} \approx \sqrt {48.88} \approx 6,99\).
Xét mẫu số liệu về chiều cao của học sinh tổ 1:
\(\overline {{x_1}} = \frac{{3 \cdot 152,5 + 2 \cdot 157,5 + 2 \cdot 162,5 + 1 \cdot 167,5 + 3 \cdot 172,5}}{{11}} \approx 162,05\).
\(s_1^2 = \frac{{3 \cdot 152,{5^2} + 2 \cdot 157,{5^2} + 2 \cdot 162,{5^2} + 1 \cdot 167,{5^2} + 3 \cdot 172,{5^2}}}{{11}} - 162,{05^2} \approx 59,68\).
\({s_1} \approx \sqrt {59,68} \approx 7,73\). Ta thấy \({s_1} > {s_2}\).
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
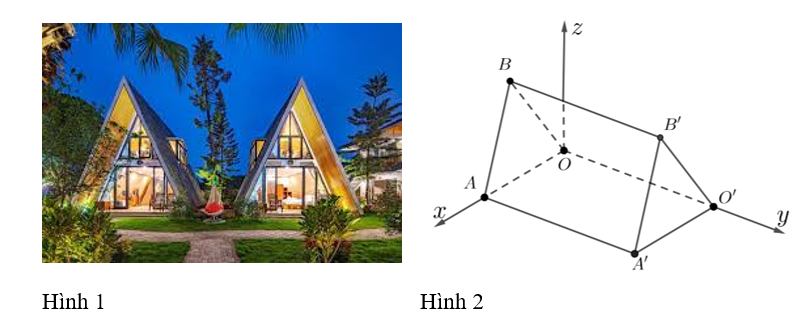
Vì điểm \(A'\) có toạ độ là \(\left( {240;450;0} \right)\) nên khoảng cách từ \(A'\) đến các trục \(Ox,Oy\) lần lượt là \(450\;{\rm{cm}}\) và \(240\;{\rm{cm}}\). Suy ra \(A'A = 450\;{\rm{cm}}\) và \(A'O' = 240\;{\rm{cm}}\).
Từ giả thiết suy ra \(\overrightarrow {A'B'} = \left( { - 120;0;300} \right)\),
do đó \(A'B' = \left| {\overrightarrow {A'B'} } \right| = \sqrt {{{( - 120)}^2} + {0^2} + {{300}^2}} = 60\sqrt {29} \approx 323(\;{\rm{cm}})\).
Vì \(O'O = A'A = 450\;{\rm{cm}}\) và \(O'\) nằm trên trục \[Oy\] nên toạ độ của điểm \(O'\) là \(\left( {0;450;0} \right)\).
Do đó \(\overline {O'B'} = \left( {120;0;300} \right)\) và \(O'B' = \left| {\overline {O'B'} } \right| = \sqrt {{{120}^2} + {0^2} + {{300}^2}} = 60\sqrt {29} \approx 323{\rm{ }}({\rm{cm}})\).
Vậy mỗi căn lều gỗ có chiều dài là \(450\;{\rm{cm}}\), chiều rộng là \(240\;{\rm{cm}}\), mỗi cạnh bên của mặt tiền có độ dài là 323 cm.
\( \Rightarrow a + b + c = 1013\).
Lời giải
Ta có \(N'\left( t \right) = - 3{t^2} + 24t = 0 \Leftrightarrow \left[ \begin{array}{l}t = 0\\t = 8\end{array} \right.\).
Bảng biến thiên
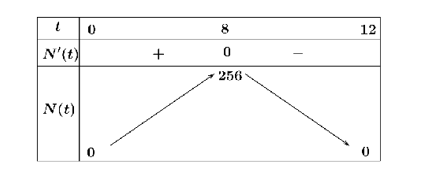
Từ bảng biến thiên ta thấy số người bị nhiễm bệnh tăng trong khoảng thời gian \(\left( {0;8} \right)\).
Suy ra \(a = 0;b = 8\). Vậy \(a + b = 8\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận