Câu hỏi:
23/12/2024 114
Cho một vật có khối lượng 10 kg đặt lên mặt sàn nằm ngang. Một người tác dụng một lực 30 N kéo vật theo phương ngang, hệ số ma sát trượt giữa vật và sàn có giá trị 0,2. Lấy giá trị của gia tốc trọng trường là 9,8 m/s2. Tính gia tốc của vật.
Cho một vật có khối lượng 10 kg đặt lên mặt sàn nằm ngang. Một người tác dụng một lực 30 N kéo vật theo phương ngang, hệ số ma sát trượt giữa vật và sàn có giá trị 0,2. Lấy giá trị của gia tốc trọng trường là 9,8 m/s2. Tính gia tốc của vật.
Câu hỏi trong đề: 13 bài tập Chủ đề 2. Động lực học có lời giải !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
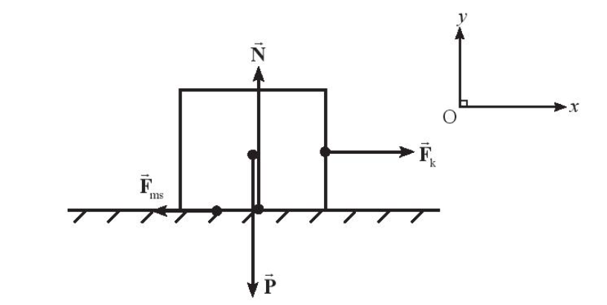
Chọn hệ quy chiếu Oxy sao cho chiều dương (+) Ox là chiều chuyển động, Oy vuông góc với Ox. Áp dụng định luật II Newton: \[\overrightarrow {{F_k}} + \overrightarrow {{F_{ms}}} + \overrightarrow N + \overrightarrow P = m.\overrightarrow a \]
Chiếu lên trục Oy: \[N - P = 0 \Rightarrow N = P = mg = 98\,\left( N \right) \Rightarrow {F_{ms}} = \mu .N = 0,2.98 = 19,6N\]
Chiếu lên trục Ox: \[{F_k} - {F_{ms}} = m.a \Rightarrow 30 - 19,6 = 10.a\]
Từ đây, ta có: a = 1,04 m/s2
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 500 Bài tập tổng ôn Vật lí (Form 2025) ( 38.000₫ )
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
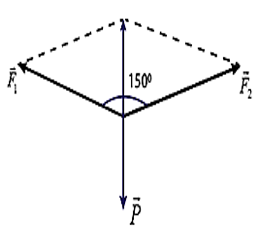
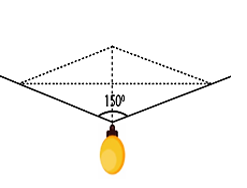
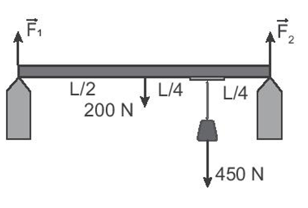
Vì bóng đèn đang nằm cân bằng nên: \({\vec T_1} + {\vec T_2} + \vec P = \vec 0\)
- Điểm treo bóng đèn nằm chính giữa dây: T1 = T2 = T
- Độ hợp lực của \({\vec T_1}\) và \({\vec T_2}\) là:\({T_{12}} = 2Tcos\frac{{{{150}^0}}}{2} = 2Tcos{75^0}\)
- Từ điều kiện cân bằng, ta có:
\({T_{12}} = P = 2T\cos {75^0} \Rightarrow T = \frac{P}{{2\cos {{75}^0}}} = \frac{{100}}{{2\cos {{75}^0}}} \approx 193,2N\)
Lời giải
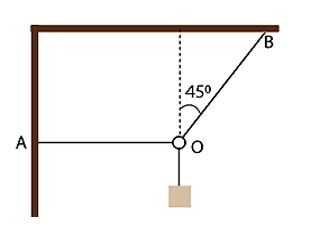
- Chọn hệ trục Oxy như hình vẽ
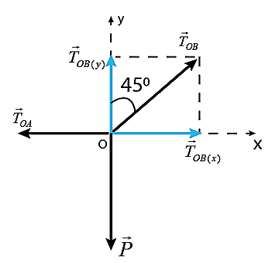
- Vòng nhẫn được giữ cân bằng tại O nên:
\({\vec T_{OA}} + {\vec T_{OB}} + \vec P = \vec 0\) (1)
- Chiều (1)/Oy, ta có:
\(T{}_{OB\left( y \right)} - P = 0 \Rightarrow T.cos{45^0} = P \Rightarrow {T_{OB}} = \frac{P}{{cos{{45}^0}}} = 20\sqrt 2 N\)
- Chiếu (1) lên Ox, ta có:
\(T{}_{OB\left( x \right)} - {T_{OA}} = 0 \Rightarrow {T_{OA}} = {T_{OB}}.\sin {45^0} = 20N\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi thử tốt nghiệp THPT môn Vật lí Sở Giáo dục và Đào tạo Nam Định có đáp án
-
(2025 mới) Đề ôn thi tốt nghiệp THPT Vật lí (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 3)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 4)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 2)
-
Đề thi thử tốt nghiệp THPT môn Vật lí THPT Yên Lạc - Vĩnh Phúc - Lần 1 có đáp án
-
(2025 mới) Đề ôn thi tốt nghiệp THPT Vật lí (Đề số 6)
-
Đề thi thử tốt nghiệp THPT môn Vật lí THPT Trưng Yên - Hưng Yên có đáp án