Câu hỏi:
23/12/2024 1,095
Con lắc đạn đạo là thiết bị được sử dụng để đo tốc độ của viên đạn. Viên đạn được bắn vào một khối gỗ lớn treo lơ lửng bằng dây nhẹ, không dãn. Sau khi va chạm, viên đạn ghim vào trong khối gỗ. Sau đó, toàn bộ hệ khối gỗ và viên đạn chuyển động như một con lắc lên độ cao h (Hình vẽ). Xét viên đạn có khối lượng m1 = 5 g, khối gỗ có khối lượng m2 = 1 kg và h = 5 cm. Lấy g = 9,8 m/s2. Bỏ qua lực cản của không khí.
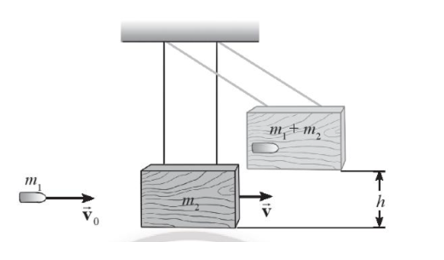
a. Tính vận tốc của hệ sau khi viên đạn ghim vào khối gỗ.
b. Tính tốc độ ban đầu của viên đạn.
Con lắc đạn đạo là thiết bị được sử dụng để đo tốc độ của viên đạn. Viên đạn được bắn vào một khối gỗ lớn treo lơ lửng bằng dây nhẹ, không dãn. Sau khi va chạm, viên đạn ghim vào trong khối gỗ. Sau đó, toàn bộ hệ khối gỗ và viên đạn chuyển động như một con lắc lên độ cao h (Hình vẽ). Xét viên đạn có khối lượng m1 = 5 g, khối gỗ có khối lượng m2 = 1 kg và h = 5 cm. Lấy g = 9,8 m/s2. Bỏ qua lực cản của không khí.
a. Tính vận tốc của hệ sau khi viên đạn ghim vào khối gỗ.
b. Tính tốc độ ban đầu của viên đạn.
Câu hỏi trong đề: 4 bài tập Chủ đề 4. Động lượng có lời giải !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a. Chọn gốc thế năng tại vị trí thấp nhất của con lắc
Áp dụng định luật bảo toàn cơ năng cho hệ ngay sau khi va chạm cho đến khi con lắc đạt độ cao cực đại: \[\frac{1}{2}\left( {{m_1} + {m_2}} \right).{v^2} = \left( {{m_1} + {m_2}} \right).g.h\]\[ \Rightarrow v = \sqrt {2g.h} = \sqrt {2.9,8.0,05} \approx 0,99m/s\]
b. Áp dụng định luật bảo toàn động lượng cho hệ khối gỗ - viên đạn ngay trước và sau va chạm: \[{m_1}.\overrightarrow {{v_0}} = \left( {{m_1} + {m_2}} \right).\overrightarrow v \]\[ \Rightarrow \overrightarrow {{v_0}} = \frac{{\left( {{m_1} + {m_2}} \right).\overrightarrow v }}{{{m_1}}}\]
Ta có độ lớn: \[{v_0} = \frac{{\left( {{m_1} + {m_2}} \right).v}}{{{m_1}}} \approx 198,99m/s\]
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 1000 câu hỏi lí thuyết môn Vật lí (Form 2025) ( 45.000₫ )
- 500 Bài tập tổng ôn Vật lí (Form 2025) ( 38.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Động lượng của hai vật lần lượt có độ lớn:
\[{p_1} = {m_1}.{v_1} = 0,4kg.m/s\]; \[{p_2} = {m_2}.{v_2} = 0,3kg.m/s\]; Động lượng của hệ: \[\overrightarrow p = \overrightarrow {{p_1}} + \overrightarrow {{p_2}} \]
a. Hình vẽ
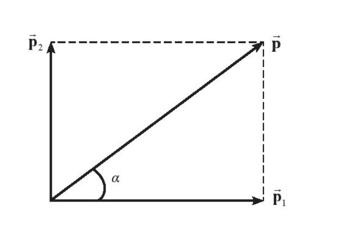
\[p = \sqrt {p_1^2 + p_2^2} = 0,5kg.m/s\]
\[\tan \alpha = \frac{{{p_2}}}{{{p_1}}} \Rightarrow \alpha \approx 37^\circ \]
(\[\overrightarrow p \] hợp với \[\overrightarrow {{p_1}} \] một góc 370)
b. Hình vẽ
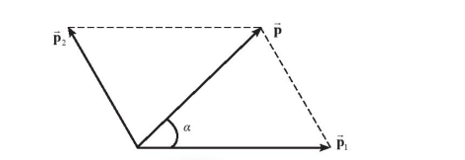
\[p = \sqrt {p_1^2 + p_2^2 + 2{p_1}{p_2}.\cos \theta } \approx 0,36kg.m/s\]
\[\cos \alpha = \frac{{{p^2} + p_1^2 - p_2^2}}{{2p.{p_1}}} = 0,7\]\[ \Rightarrow \alpha = 46^\circ \](\[\overrightarrow p \] hợp với \[\overrightarrow {{p_1}} \] một góc 460)
Lời giải
a) Động lượng của vận động viên khi bắt đầu thả rơi là: \[{p_1} = m.{v_1} = 60.0 = 0kg.m/s\]
Vận tốc rơi tự do của vận động viên khi chạm mặt nước là: \[v = \sqrt {2gh} = \sqrt {2.10.4,5} = 3\sqrt {10} m/s\]
Động lượng của vận động viên khi chạm mặt nước là: \[{p_2} = m.{v_2} = 60.3\sqrt {10} = 180\sqrt {10} kg.m/s\]
b) Lực cản mà nước tác dụng lên người vận động viên là: \[{F_c} = \frac{{\Delta p}}{{\Delta t}} = \frac{{0 - 180\sqrt {10} }}{{0,5}} \approx - 1138,42N\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo