Một viên đạn pháo khối lượng m1 = 10 kg bay ngang với vận tốc v1 = 500 m/s dọc theo đường sắt và cắm vào toa xe chở cát có khối lượng m2 = 1 tấn, đang chuyển động với tốc độ v2 = 36 km/h. Xác định vận tốc của toa xe ngay sau khi trúng đạn trong hai trường hợp:
a. Đạn bay đến cùng chiều chuyển động của xe cát.
b. Đạn bay đến ngược chiều chuyển động của xe cát.
Một viên đạn pháo khối lượng m1 = 10 kg bay ngang với vận tốc v1 = 500 m/s dọc theo đường sắt và cắm vào toa xe chở cát có khối lượng m2 = 1 tấn, đang chuyển động với tốc độ v2 = 36 km/h. Xác định vận tốc của toa xe ngay sau khi trúng đạn trong hai trường hợp:
a. Đạn bay đến cùng chiều chuyển động của xe cát.
b. Đạn bay đến ngược chiều chuyển động của xe cát.
Câu hỏi trong đề: 4 bài tập Chủ đề 4. Động lượng có lời giải !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn chiều chuyển động ban đầu của xe cát là chiều dương, hệ vật gồm xe cát và đạn chuyển động theo phương ngang.
a. Đổi: \[{v_2} = 36km/h = 10m/s\]
Va chạm giữa viên đạn và toa xe là va chạm mềm nên động lượng của hệ (đạn + xe) là không đổi: \[{m_1}\overrightarrow {{v_1}} + {m_2}\overrightarrow {{v_2}} = \left( {{m_1} + {m_2}} \right)\overrightarrow v \]
Do \[\overrightarrow {{v_1}} \uparrow \uparrow \overrightarrow {{v_2}} \]\[ \Rightarrow v = \frac{{{m_1}{v_1} + {m_1}{v_2}}}{{{m_1} + {m_2}}} = \frac{{10.500 + 1000.10}}{{10 + 1000}} \approx 14,85m/s\]
b. Khi đạn bay đến ngược chiều xe cát (\[\overrightarrow {{v_1}} \uparrow \downarrow \overrightarrow {{v_2}} \]) thì ta có:
\[v = \frac{{{m_1}{v_1} + {m_1}{v_2}}}{{{m_1} + {m_2}}} = \frac{{10.\left( { - 500} \right) + 1000.10}}{{10 + 1000}} \approx 4,95m/s\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Động lượng của hai vật lần lượt có độ lớn:
\[{p_1} = {m_1}.{v_1} = 0,4kg.m/s\]; \[{p_2} = {m_2}.{v_2} = 0,3kg.m/s\]; Động lượng của hệ: \[\overrightarrow p = \overrightarrow {{p_1}} + \overrightarrow {{p_2}} \]
a. Hình vẽ
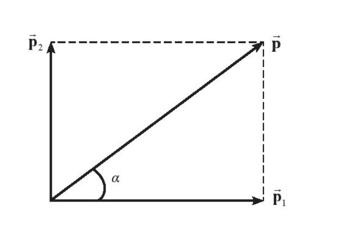
\[p = \sqrt {p_1^2 + p_2^2} = 0,5kg.m/s\]
\[\tan \alpha = \frac{{{p_2}}}{{{p_1}}} \Rightarrow \alpha \approx 37^\circ \]
(\[\overrightarrow p \] hợp với \[\overrightarrow {{p_1}} \] một góc 370)
b. Hình vẽ
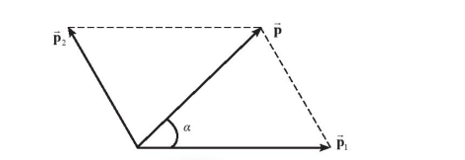
\[p = \sqrt {p_1^2 + p_2^2 + 2{p_1}{p_2}.\cos \theta } \approx 0,36kg.m/s\]
\[\cos \alpha = \frac{{{p^2} + p_1^2 - p_2^2}}{{2p.{p_1}}} = 0,7\]\[ \Rightarrow \alpha = 46^\circ \](\[\overrightarrow p \] hợp với \[\overrightarrow {{p_1}} \] một góc 460)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
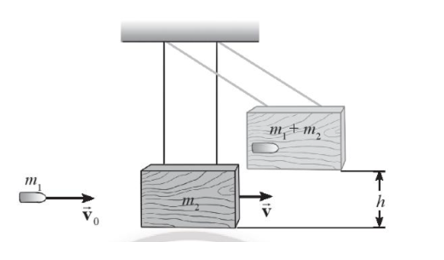
a. Chọn gốc thế năng tại vị trí thấp nhất của con lắc
Áp dụng định luật bảo toàn cơ năng cho hệ ngay sau khi va chạm cho đến khi con lắc đạt độ cao cực đại: \[\frac{1}{2}\left( {{m_1} + {m_2}} \right).{v^2} = \left( {{m_1} + {m_2}} \right).g.h\]\[ \Rightarrow v = \sqrt {2g.h} = \sqrt {2.9,8.0,05} \approx 0,99m/s\]
b. Áp dụng định luật bảo toàn động lượng cho hệ khối gỗ - viên đạn ngay trước và sau va chạm: \[{m_1}.\overrightarrow {{v_0}} = \left( {{m_1} + {m_2}} \right).\overrightarrow v \]\[ \Rightarrow \overrightarrow {{v_0}} = \frac{{\left( {{m_1} + {m_2}} \right).\overrightarrow v }}{{{m_1}}}\]
Ta có độ lớn: \[{v_0} = \frac{{\left( {{m_1} + {m_2}} \right).v}}{{{m_1}}} \approx 198,99m/s\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập