Một sóng truyền trên dây đàn hồi có biên độ bằng 6 cm, tần số bằng 16 Hz và có tốc độ truyền bằng 8,0 m/s. Phương trình truyền sóng có thể là
A. \(u = 6{\rm{cos}}\left( {32\pi t - 4\pi x} \right)\left( {{\rm{cm}}} \right)\) (x được tính theo m, t được tính theo s).
B. \(u = 6{\rm{cos}}\left( {16\pi t - 4\pi x} \right)\left( {{\rm{cm}}} \right)\) (x được tính theo m, t được tính theo s).
C. \(u = 6{\rm{cos}}\left( {32\pi t - 4\pi x} \right)\left( {{\rm{cm}}} \right)\) (x được tính theo m, t được tính theo s).
Câu hỏi trong đề: 17 bài tập Chủ đề 2. Sóng có lời giải !!
Quảng cáo
Trả lời:
Ta có: \(\lambda = \frac{{8,0}}{{16}} = 0,50{\rm{\;m}} \Rightarrow u = A{\rm{cos}}\left( {2\pi ft - \frac{{2\pi }}{\lambda }x} \right) = 6{\rm{cos}}\left( {32\pi t - 4\pi x} \right)\left( {{\rm{cm}}} \right)\) với x được tính bằng m. Chọn A.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 1000 câu hỏi lí thuyết môn Vật lí (Form 2025) ( 45.000₫ )
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Ta có: \(I = \frac{{25,0}}{{4\pi {{\left( {2,02 \cdot {{10}^7}} \right)}^2}}} \approx 4,88 \cdot {10^{ - 15}}{\rm{\;W/}}{{\rm{m}}^{\rm{2}}}\).
b) Bước sóng của tín hiệu mà trạm thu sóng nhận được là: \(\lambda = \frac{{3,{{0.10}^8}}}{{1575,42 \cdot {{10}^6}}} \approx 0,19{\rm{\;m}}.\)
Lời giải
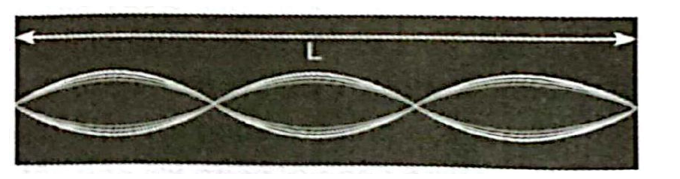
a) Trên hình vẽ các định được k = 3:
\(L = 3\frac{\lambda }{2} \Rightarrow \lambda = \frac{{2.{\rm{L}}}}{3} = \frac{{2 \cdot 0,9}}{3} = 0,6{\rm{\;m}}\).
b) \(v = \lambda f = 0,6.180 = 108{\rm{\;m}}/{\rm{s}}\).
c) \(\left. {\begin{array}{*{20}{l}}{{v_1} = {f_1}{\lambda _1}}\\{{v_2} = {f_2}{\lambda _2}}\end{array}} \right\} \Rightarrow \frac{{{f_1}{\lambda _1}}}{{{f_2}{\lambda _2}}} = 1 \Rightarrow {\lambda _2} = \frac{{{f_1}{\lambda _1}}}{{{f_2}}} = \frac{{180 \cdot 0,6}}{{360}} = 0,3{\rm{\;m}}\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.