Cho tam giác ABC vuông tại A có AB = 30 cm và tanB = \(\frac{5}{{12}}\). Độ dài cạnh BC là
A. 12,5 cm.
B. 32,5 cm.
C. 30 cm.
D. 22,5 cm.
Quảng cáo
Trả lời:
Đáp án đúng là: B
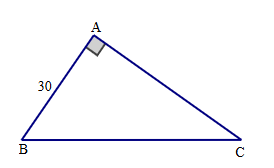
Ta có:
tanB = \(\frac{5}{{12}}\) hay \(\frac{{AC}}{{AB}} = \frac{5}{{12}}\) suy ra AC = \(\frac{5}{{12}}\).BA = 12,5 cm.
Áp dụng định lí Pythagore vào tam giác ABC, ta có:
AB2 + AC2 = BC2
302 + 12,52 = BC2
Suy ra BC =32,5 cm.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. 27 cm.
B. 48 cm.
C. 25 cm.
D. 21 cm.
Lời giải
Đáp án đúng là: C
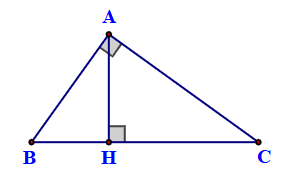
Ta có: SABH.SACH = 54.96
Suy ra \(\frac{1}{4}\)AB2.BH.CH = 54.96
AH4 = 4.54.96 = 124
Suy ra AH = 12.
Lại có SABC = \(\frac{1}{2}AH.BC\)
Suy ra BC = \(\frac{{2{S_{ABC}}}}{{AH}} = \frac{{2\left( {54 + 96} \right)}}{{12}} = 25\) (cm).
Câu 2
A. 10,79 cm2.
B. 11 cm2.
C. 10,8 cm2.
D. 10,795 cm2.
Lời giải
Đáp án đúng là: B
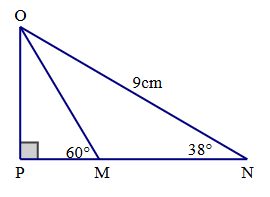
Xét tam giác OPN vuông tại P nên ta có:
OP = ON.sin\(\widehat N\) = 9.sin 38° ≈ 5,54 (cm).
NP = ON.cos\(\widehat N\) = 9.cos 38° ≈ 7,09 (cm).
Xét tam giác OPM vuông tại P nên ta có:
MP = \(\frac{{OP}}{{\tan \widehat M}} = \frac{{5,54}}{{\tan 60^\circ }} = \frac{{5,54}}{{\sqrt 3 }} = 3,2\) (cm).
Ta có: MN = NP – MP = 7,09 – 3,2 – 3,89 (cm).
Do đó, SOMN = \(\frac{1}{2}OP.MN = \frac{1}{2}.5,55.3,89 \approx 11\) cm2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. 10,3 cm.
B. 6,9 cm.
C. 10,34 cm.
D. 6,93 cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. 8,96 cm2.
B. 22,4 cm2.
C. 15 cm2.
D. 20 cm2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. 3,6 cm.
B. 7,3 cm.
C. 7,2 cm.
D. 7,5 cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.