Tâm của đường tròn ngoại tiếp tam giác vuông là:

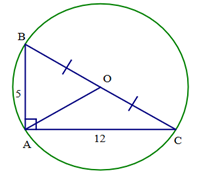
Gọi O là trung điểm BC.

Xét tam giác vuông ABC, có AO là trung tuyến nên AO = \(\frac{1}{2}\)BC.

Suy ra OA = OB = OC.

Do đó ba điểm A, B, C cùng thuộc một đường tròn tâm O bán kính \(\frac{1}{2}\)BC.

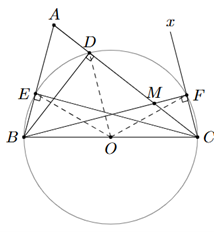
Gọi O là trung điểm của BC.

Ta có: BD là đường cao nên BD ⊥ AC, hay tam giác BDC vuông tại D.

Trong tam giác vuông BDC có DO là trung tuyến ứng với cạnh huyền BC nên

OD = OB = OC = \(\frac{1}{2}\)BC (1).

Tương tự, ta có: OE = OB = OC = \(\frac{1}{2}\)BC  (2) và OF = OB = OC = \(\frac{1}{2}\)BC  (3).

Do đó, năm điểm B, C, D, E, F cùng thuộc một đường tròn (O; R) với R = \(\frac{1}{2}\)BC.