Câu hỏi:
12/04/2025 149
Câu 1-2. (2,0 điểm) Biểu đồ dưới đây biểu diễn tỉ lệ về thời gian chạy cự li 100 mét của các học sinh lớp 9A.
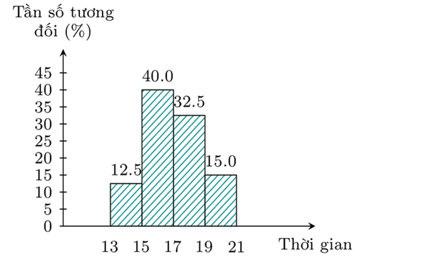
Biết rằng có 5 học sinh có thời gian chạy từ 13 giây đến dưới 15 giây.
a) Lập bảng tần số ghép nhóm tương ứng.
Câu 1-2. (2,0 điểm) Biểu đồ dưới đây biểu diễn tỉ lệ về thời gian chạy cự li 100 mét của các học sinh lớp 9A.
Biết rằng có 5 học sinh có thời gian chạy từ 13 giây đến dưới 15 giây.
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Gọi \(n\) là tổng số học sinh của lớp 9A, ta có \(\frac{5}{n} \cdot 100\% = 12,5\% \).
Suy ra \(n = 40\) học sinh.
Ta có bảng phân bố tần số ghép nhóm như sau:
|
Thời gian (tính bằng giây) |
\(\left[ {13;15} \right)\) |
\(\left[ {15;17} \right)\) |
\(\left[ {17;19} \right)\) |
\(\left[ {19;21} \right)\) |
|
Tần số |
5 |
16 |
13 |
6 |
Câu hỏi cùng đoạn
Câu 2:
b) Bạn lớp trưởng cho rằng có trên 50% số học sinh của lớp có thời gian chạy nhanh hơn 17 giây. Nhận định đó đúng hay sai? Tại sao?
Lời giải của GV VietJack
b) Tổng số học sinh chạy nhanh hơn 17 giây là 19 học sinh, đạt tỉ lệ \(\frac{{19}}{{40}} \cdot 100\% = 47,5\% .\)Do đó nhận định của bạn lớp trưởng là nhận định sai.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Ta có bảng sau:
|
Lần 2 Lần 1 |
1 |
2 |
3 |
4 |
|
1 |
(1, 1) |
(1, 2) |
(1, 3) |
(1, 4) |
|
2 |
(2, 1) |
(2, 2) |
(2, 3) |
(2, 4) |
|
3 |
(3, 1) |
(3, 2) |
(3, 3) |
(3, 4) |
|
4 |
(4, 1) |
(4, 2) |
(4, 3) |
(4, 4) |
Không gian mẫu là:
\[\Omega = \left\{ {\left( {1\,,\,\,1} \right)\,;\,\,\left( {1\,,\,\,2} \right)\,;\,\,\left( {1\,,\,\,3} \right)\,;\,\,\left( {1\,,\,\,4} \right)\,;\,\,\left( {2\,,\,\,1} \right)\,;\,\,\left( {2\,,\,\,2} \right);{\rm{ }}\left( {2\,,\,\,3} \right);{\rm{ }}\left( {2\,,\,\,4} \right);{\rm{ }}\left( {3\,,\,\,1} \right)\,;\,\,\left( {3\,,\,\,2} \right)} \right.\,;\,\,\left( {3\,,\,\,3} \right)\,;\,\,\left( {3\,,\,\,4} \right)\,;{\rm{ }}\] \[\left. {\left( {4\,,\,\,1} \right);\,\,\left( {4\,,\,\,2} \right);\,\,\left( {4\,,\,\,3} \right);\,\,\left( {4\,,\,\,4} \right)} \right\}.\]
Do đó, không gian mẫu có 16 phần tử.
Lời giải
a) Đường kính của hình nón là: \[26 - 2{\rm{ }}.{\rm{ }}3 = 20{\rm{ }}\left( {{\rm{cm}}} \right)\].
Bán kính \[r = \frac{{20}}{2} = 10{\rm{ }}\left( {{\rm{cm}}} \right)\].
Đường sinh là \[30{\rm{ cm}}\].
Vậy diện tích xung quanh của hình nón là:
\[{S_{xq}} = \pi rl = \pi \cdot 10 \cdot 30 = 300\pi {\rm{ }}\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right) \approx 942,48{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\].
Để phủ kín mặt ngoài chiếc mũ của chú hề, số giấy màu cần dùng là khoảng \[942,48{\rm{ c}}{{\rm{m}}^{\rm{2}}}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Chuyên đề 8: Hình học (có đáp án)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận