Câu hỏi:
12/04/2025 247
Câu 3-4. (1,5 điểm) Một tấm bìa cứng hình tròn được chia làm bốn hình quạt bằng nhau, đánh số 1; 2; 3; 4 và được gắn vào trục quay có mũi tên ở tâm (hình vẽ).
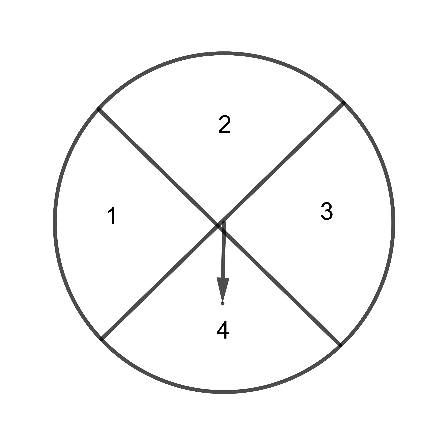
Bạn Tuấn quay tấm bìa hai lần, quan sát và ghi lại số hình quạt và mũi tên chỉ vào.
a) Xác định không gian mẫu của không gian mẫu.
Câu 3-4. (1,5 điểm) Một tấm bìa cứng hình tròn được chia làm bốn hình quạt bằng nhau, đánh số 1; 2; 3; 4 và được gắn vào trục quay có mũi tên ở tâm (hình vẽ).
Bạn Tuấn quay tấm bìa hai lần, quan sát và ghi lại số hình quạt và mũi tên chỉ vào.
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Ta có bảng sau:
|
Lần 2 Lần 1 |
1 |
2 |
3 |
4 |
|
1 |
(1, 1) |
(1, 2) |
(1, 3) |
(1, 4) |
|
2 |
(2, 1) |
(2, 2) |
(2, 3) |
(2, 4) |
|
3 |
(3, 1) |
(3, 2) |
(3, 3) |
(3, 4) |
|
4 |
(4, 1) |
(4, 2) |
(4, 3) |
(4, 4) |
Không gian mẫu là:
\[\Omega = \left\{ {\left( {1\,,\,\,1} \right)\,;\,\,\left( {1\,,\,\,2} \right)\,;\,\,\left( {1\,,\,\,3} \right)\,;\,\,\left( {1\,,\,\,4} \right)\,;\,\,\left( {2\,,\,\,1} \right)\,;\,\,\left( {2\,,\,\,2} \right);{\rm{ }}\left( {2\,,\,\,3} \right);{\rm{ }}\left( {2\,,\,\,4} \right);{\rm{ }}\left( {3\,,\,\,1} \right)\,;\,\,\left( {3\,,\,\,2} \right)} \right.\,;\,\,\left( {3\,,\,\,3} \right)\,;\,\,\left( {3\,,\,\,4} \right)\,;{\rm{ }}\] \[\left. {\left( {4\,,\,\,1} \right);\,\,\left( {4\,,\,\,2} \right);\,\,\left( {4\,,\,\,3} \right);\,\,\left( {4\,,\,\,4} \right)} \right\}.\]
Do đó, không gian mẫu có 16 phần tử.
Câu hỏi cùng đoạn
Câu 2:
b) Tính xác suất của các biến cố:
E: “Tổng hay số ghi trên hai hình quạt ở hai lần quay bằng 5”.
F: “Tích hai số ghi trên hai hình quạt ở hai lần quay bằng 4”.
b) Tính xác suất của các biến cố:
E: “Tổng hay số ghi trên hai hình quạt ở hai lần quay bằng 5”.
F: “Tích hai số ghi trên hai hình quạt ở hai lần quay bằng 4”.
Lời giải của GV VietJack
b) Có 4 kết quả thuận lợi cho biến cố \(E\) là \[E = \left\{ {\left( {1\,,\,\,4} \right)\,;\,\,\left( {2\,,\,\,3} \right)\,;\,\,\left( {3\,,\,\,2} \right)\,;\,\,\left( {4\,,\,\,1} \right)} \right\}.\]
Do đó, xác suất của biến cố \(E\) là \(P\left( E \right) = \frac{4}{{16}} = \frac{1}{4}.\)
b) Có 3 kết quả thuận lợi cho biến cố \(F\) là \[F = \left\{ {\left( {1\,,\,\,4} \right)\,;\,\,\left( {2\,,\,\,2} \right)\,;\,\,\left( {4\,,\,\,1} \right)} \right\}.\]
Do đó, xác suất của biến cố \(F\) là \(P\left( F \right) = \frac{3}{{16}}.\)
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Gọi \(n\) là tổng số học sinh của lớp 9A, ta có \(\frac{5}{n} \cdot 100\% = 12,5\% \).
Suy ra \(n = 40\) học sinh.
Ta có bảng phân bố tần số ghép nhóm như sau:
|
Thời gian (tính bằng giây) |
\(\left[ {13;15} \right)\) |
\(\left[ {15;17} \right)\) |
\(\left[ {17;19} \right)\) |
\(\left[ {19;21} \right)\) |
|
Tần số |
5 |
16 |
13 |
6 |
Lời giải
a) Đường kính của hình nón là: \[26 - 2{\rm{ }}.{\rm{ }}3 = 20{\rm{ }}\left( {{\rm{cm}}} \right)\].
Bán kính \[r = \frac{{20}}{2} = 10{\rm{ }}\left( {{\rm{cm}}} \right)\].
Đường sinh là \[30{\rm{ cm}}\].
Vậy diện tích xung quanh của hình nón là:
\[{S_{xq}} = \pi rl = \pi \cdot 10 \cdot 30 = 300\pi {\rm{ }}\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right) \approx 942,48{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\].
Để phủ kín mặt ngoài chiếc mũ của chú hề, số giấy màu cần dùng là khoảng \[942,48{\rm{ c}}{{\rm{m}}^{\rm{2}}}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Chuyên đề 8: Hình học (có đáp án)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận