Câu hỏi:
12/04/2025 75
Cho tứ giác ABCD. Chứng minh diện tích của tứ giác ABCD không lớn hơn \(\frac{{AB \cdot BC + AD \cdot DC}}{2}{\rm{. }}\)
Cho tứ giác ABCD. Chứng minh diện tích của tứ giác ABCD không lớn hơn \(\frac{{AB \cdot BC + AD \cdot DC}}{2}{\rm{. }}\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
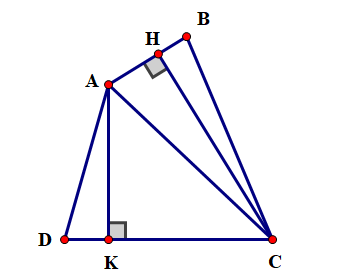
Kẻ CH vuông góc với AB tại H, A K vuông góc với DC tại \(K\). Khi đó, diện tích của tam giác ABC là: \({S_1} = \frac{{AB \cdot CH}}{2}\) và diện tích của tam giác ACD là: \({S_2} = \frac{{DC \cdot AK}}{2}\).
Diện tích của tứ giác ABCD là: \(S = {S_1} + {S_2} = \frac{{AB \cdot CH + AK \cdot DC}}{2}.\)
Mà \(CH \le BC\) và \(AK \le AD\), suy ra\(S \le \frac{{AB \cdot BC + AD \cdot DC}}{2}.\)
Vậy diện tích của tứ giác ABCD không lớn hơn \(\frac{{AB \cdot BC + AD \cdot DC}}{2}\).
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(x\) là số chiếc bánh tẻ mà bà Mai gói \(\left( {x \in {\mathbb{N}^*}} \right)\).
Khi đó, tổng thời gian bà Mai dùng để gói hai loại bánh là: \(3x + 2.75\) (phút).
Do bà Mai dành không quá 4 giờ để gói hai loại bánh nên ta có bất phương trình: \(3x + 2.75 \le 4.60.{\rm{ }}\)
Giải bất phương trình trên: \(3x + 2.75 \le 4.60\)
\(3x + 150 \le 240\)
\(3x \le 90\)
\(x \le 30.\)
Vậy bà Mai có thể gói được nhiều nhất 30 chiếc bánh tẻ.
Lời giải
Gọi \(x(\;{\rm{m}})\) là độ dài cạnh song song với bờ giậu và \(y(\;{\rm{m}})\) là độ dài cạnh vuông góc với bờ giậu \((x > 0,y > 0)\). Khi đó, ta có: \(x + 2y = 80\) hay \(x = 80 - 2y\).
Diện tích của mảnh vườn là:
\(S = xy = (80 - 2y)y = - 2{y^2} + 80y = - 2\left( {{y^2} - 40y + 400} \right) + 800\)\( = - 2{(y - 20)^2} + 800\left( {\;{{\rm{m}}^2}} \right).\)
Do \({(y - 20)^2} \ge 0\) với số \(y\) tuỳ ý nên \( - 2{(y - 20)^2} + 800 \le 800\). Do đó, diện tích lớn nhất của mảnh vườn mà bác Long rào được là \(800\;{{\rm{m}}^2}\). Dấu "=" xảy ra khi \(y - 20 = 0\) hay \(y = 20\). Thay \(y = 20\) vào \(x = 80 - 2y\), ta được: \(x = 80 - 2 \cdot 20 = 40\).
Vậy mảnh vườn có diện tích lớn nhất mà bác Long rào được có chiều dài 40 m và chiều rộng 20 m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đắk Lắk
-
123 bài tập Nón trụ cầu và hình khối có lời giải
-
50 bài tập Một số yếu tố xác suất có lời giải
-
Đề thi tham khảo môn Toán vào 10 tỉnh Quảng Bình năm học 2025-2026
-
Đề thi minh họa (Dự thảo) TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đồng Nai
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_TP Hà Nội
-
Đề thi thử TS vào 10 (Lần 2 - Tháng 2) năm học 2025 - 2026_Môn Toán_THCS Hoằng Thanh_Tỉnh Thanh Hóa
-
Đề thi tham khảo TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Bình Phước
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận