(1,0 điểm) Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình.
Tiền cước điện thoại \(y\) (nghìn đồng) là số tiền mà người sử dụng cần trả hằng tháng, số tiền đó phụ thuộc vào thời gian gọi \(x\) (phút) của người đó trong tháng. Mối liên hệ giữa hai đại lượng này là một hàm số bậc nhất \(y = ax + b\,\,\left( {a \ne 0} \right).\) Hãy xác định hàm số trên trong trường hợp mẹ bạn An trong tháng 1/2025 đã gọi 100 phút với số tiền cước là 40 nghìn đồng và trong tháng 2/2025 đã gọi 40 phút với số tiền cước là 28 nghìn đồng.
(1,0 điểm) Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình.
Tiền cước điện thoại \(y\) (nghìn đồng) là số tiền mà người sử dụng cần trả hằng tháng, số tiền đó phụ thuộc vào thời gian gọi \(x\) (phút) của người đó trong tháng. Mối liên hệ giữa hai đại lượng này là một hàm số bậc nhất \(y = ax + b\,\,\left( {a \ne 0} \right).\) Hãy xác định hàm số trên trong trường hợp mẹ bạn An trong tháng 1/2025 đã gọi 100 phút với số tiền cước là 40 nghìn đồng và trong tháng 2/2025 đã gọi 40 phút với số tiền cước là 28 nghìn đồng.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Thay \(x = 100,\,\,y = 40\) vào công thức \(y = ax + b\) ta được \(100a + b = 40\) (1)
Thay \(x = 40,\,\,y = 28\) vào công thức \(y = ax + b\) ta được \(40a + b = 28\) (2)
Từ (1) và (2) ta có hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{100a + b = 40\,\,\,\,\left( 1 \right)}\\{40a + b = 28\,\,\,\,\,\,\left( 2 \right)}\end{array}} \right.\)
Trừ từng vế của phương trình (1) cho phương trình (2), ta được:
\(60a = 12,\) suy ra \(a = \frac{1}{5}\) (thỏa mãn).
Thay \(a = \frac{1}{5}\) vào phương trình (2), ta được: \(40 \cdot \frac{1}{5} + b = 28,\) suy ra \(b = 20.\)
Vậy hàm số bậc nhất cần tìm là \(y = \frac{1}{5}x + 20.\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
Đáp án đúng là: D
Điều kiện xác định của biểu thức \(P = 2025\sqrt {2026 - x} \) là \(2026 - x \ge 0\) tức là \(x \le 2026.\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
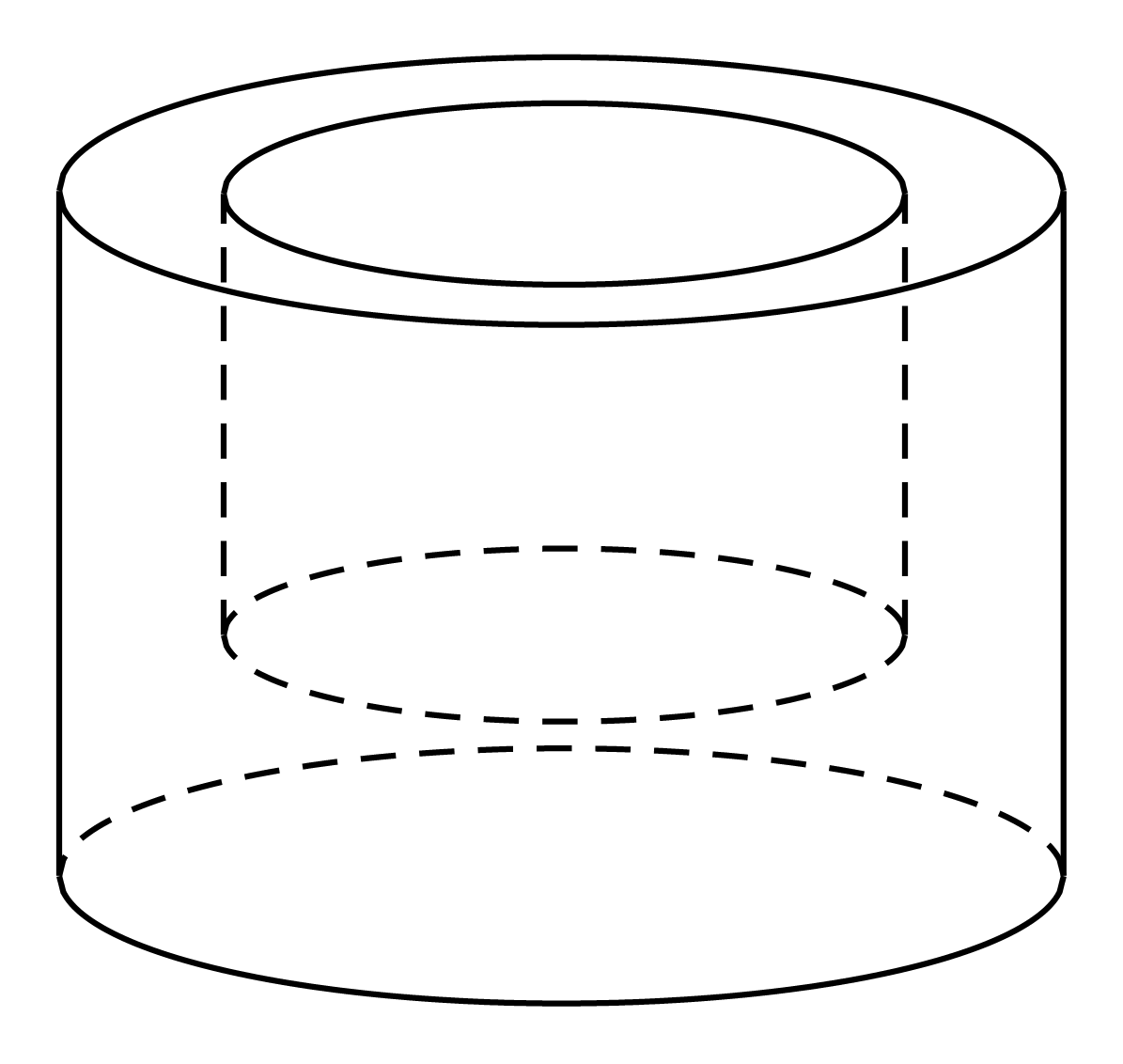
Thể tích chi tiết máy có dạng hình trụ với bán kính đáy bằng chiều cao và bằng 17 cm là:
\({V_1} = \pi r_1^2{h_1} = \pi \cdot {17^2} \cdot 17 = 4913\pi \)(cm2).
Thể tích lỗ khoan rồng có dạng hình trụ với bán kính đáy và độ sâu bằng 6 cm là:
\({V_2} = \pi r_2^2{h_2} = \pi \cdot {6^2} \cdot 6 = 216\pi \) (cm2).
Thể tích của phần chi tiết máy còn lại sau khi khoan là:
\[V = {V_1} - {V_2} = 4913\pi - 216\pi = 4697\pi = 14\,\,756,06\] (cm2).
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập