khoahoc.vietjack.com
Giảm 50% Kích hoạt VIP
khoahoc.vietjack.com
Kích hoạt VIP Đăng nhập
Tạo VIP
  2. Lớp 12
  3. Toán

Câu hỏi:

06/05/2025 31,294 Lưu

Để chuẩn bị cho một buổi triển lãm quốc tế, các trang sức có giá trị lớn được đặt bảo mật trong các khối chóp tứ giác đều S.ABCD và đặt lên phía trên một trụ hình hộp chữ nhật ABCD.A'B'C'D' có đáy là hình vuông (như hình vẽ bên).

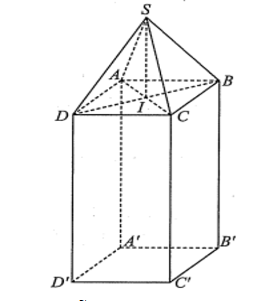
Tính giá trị của a + b + c (làm tròn kết quả đến hàng phần trăm). (ảnh 1)

 

Chọn hệ trục tọa độ Oxyz (đơn vị trên mỗi trục là mét) sao cho A'(0; 0; 0), A(0; 0; 1), \(B\left( {0;\frac{1}{2};1} \right)\). Biết rằng, ban tổ chức sự kiện dự định dùng các tấm kính cường lực hình tam giác cân có cạnh bên là 60 cm để ráp lại thành khối chóp nói trên. Khi đó, tọa độ điểm S(a; b; c). Tính giá trị của a + b + c (làm tròn kết quả đến hàng phần trăm).

A. 0,98;
B. 0,89;
C. 1,98;
D. 1,89.
Xem lời giải

Câu hỏi trong đề: Các dạng bài tập Biểu thức toạ độ của các phép toán vectơ lớp 12 (có lời giải) !!

Flashcard Bắt Đầu Thi Giao bài

Quảng cáo

Trả lời:

verified Giải bởi Vietjack

Hướng dẫn giải:

Đáp án đúng là: C

Chọn hệ trục tọa độ Oxyz như hình vẽ

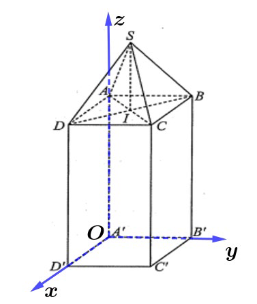
Tính giá trị của a + b + c (làm tròn kết quả đến hàng phần trăm). (ảnh 2)

Do giả thiết khối chóp tứ giác đều S.ABCD nên ABCD là hình vuông.

Có A'(0; 0; 0), A(0; 0; 1), \(B\left( {0;\frac{1}{2};1} \right)\), \(B'\left( {0;\frac{1}{2};0} \right),D'\left( {\frac{1}{2};0;0} \right)\), \(D\left( {\frac{1}{2};0;1} \right)\).

I là trung điểm của BD nên \(I\left( {\frac{1}{4};\frac{1}{4};1} \right)\).

Ta có \(BD = \frac{{\sqrt 2 }}{2};IB = ID = \frac{{\sqrt 2 }}{4};SI = \sqrt {S{B^2} - I{B^2}} = \sqrt {0,{6^2} - {{\left( {\frac{{\sqrt 2 }}{4}} \right)}^2}} = \frac{{\sqrt {94} }}{{20}}\).

Vậy \(S\left( {\frac{1}{4};\frac{1}{4};\frac{{\sqrt {94} }}{{20}} + 1} \right)\). Suy ra a + b + c ≈ 1,98.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

  • Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
  • Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
  • Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
  • Tải xuống đề thi [DOCX] với đầy đủ đáp án
  • Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
  • Bao gồm tất cả các bậc từ Tiểu học đến Đại học
  • Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
  • Đăng ký ngay
Avatar

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Với hệ trục tọa độ Oxyz sao cho O nằm trên mặt nước, mặt phẳng (Oxy) là mặt nước, trục Oz hướng lên trên (đơn vị đo: mét), một con chim bói cá đang ở vị trí cách mặt nước 2 m, cách mặt phẳng (Oxz), (Oyz) lần lượt là 3m và 1m phóng thẳng xuống vị trí con cá, biết con cá cách mặt nước 50 cm, cách mặt phẳng (Oxz), (Oyz) lần lượt là 1m và 1,5m. Tìm tọa độ điểm B lúc chim bói cá vừa tiếp xúc với mặt nước.

Tìm tọa độ điểm B lúc chim bói cá vừa tiếp xúc với mặt nước. (ảnh 1)
A. \(\left( {\frac{7}{5};\frac{7}{5};0} \right)\);
B. \(\left( {\frac{7}{5};0;0} \right)\); 
C. \(\left( {\frac{7}{5};0;\frac{7}{5}} \right)\);
D. \(\left( {0;\frac{7}{5};\frac{7}{5}} \right)\).

Lời giải

Hướng dẫn giải:

Đáp án đúng là: A

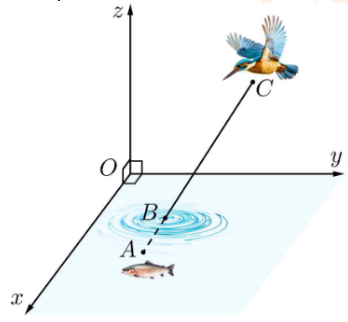
Theo đề ta có A(1,5; 1; −0,5); C(1; 3; 2); \(\overrightarrow {AC} = \left( { - 0,5;2;2,5} \right)\).

Gọi \(B\left( {x;y;0} \right)\)\( \Rightarrow \overrightarrow {AB} = \left( {x - 1,5;y - 1;0,5} \right)\).

Vì \(\overrightarrow {AB} ,\overrightarrow {AC} \) cùng phương nên \(\frac{{x - 1,5}}{{ - 0,5}} = \frac{{y - 1}}{2} = \frac{{0,5}}{{2,5}} = \frac{1}{5}\)\( \Rightarrow \left\{ \begin{array}{l}x = \frac{7}{5}\\y = \frac{7}{5}\end{array} \right.\).

 Vậy \(B\left( {\frac{7}{5};\frac{7}{5};0} \right)\).

Câu 2

Trong không gian, xét hệ tọa độ Oxyz có gốc O trùng với vị trí của một giàn khoan trên biển, mặt phẳng (Oxy) trùng với mặt biển (được coi là phẳng) với trục Ox hướng về phía tây, trục Oy hướng về phía nam và trục Oz hướng thẳng đứng lên trời. Đơn vị đo trong không gian Oxyz lấy theo km. Một chiếc ra đa đặt tại giàn khoan và một chiếc tàu thám hiểm có tọa độ là (30; 20; −15). Khoảng cách theo đơn vị km từ chiếc ra đa và một chiếc tàu thám hiểm (kết quả làm tròn lấy một chữ số thập phân).

Trong không gian, xét hệ tọa độ Oxyz có gốc O trùng với vị trí của một giàn khoan trên biển, mặt phẳng (Oxy) trùng với mặt biển (được coi là phẳng) với trục Ox hướng về phía tây, trục Oy hướn (ảnh 1)

A. 41,8 km;

B. 31,8 km;

C. 41,9 km;

D. 31,9 km.

Lời giải

Đáp án đúng là: A

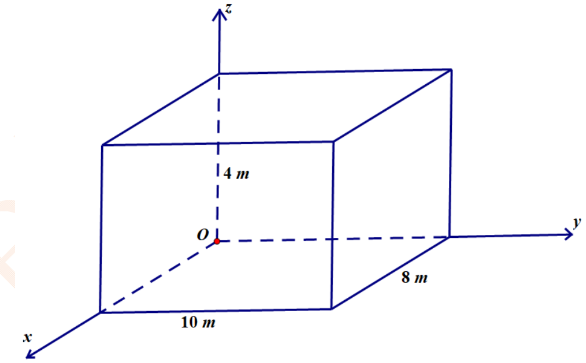
A. Theo đề bài ta có tọa độ của ra đa là (0; 0; 0), tọa độ của tàu thám hiểm là (30; 25; −15).

B. Khi đó khoảng cách giữa ra đa và tàu thám hiểm là:

C. \(d = \sqrt {{{\left( {30 - 0} \right)}^2} + {{\left( {25 - 0} \right)}^2} + {{\left( { - 15 - 0} \right)}^2}} = 5\sqrt {70} \approx 41,8\).

D. Vậy khoảng cách giữa ra đa và tàu thám hiểm là 41,8 km.

Câu 3

Một phòng học có thiết kế dạng hình hộp chữ nhật với chiều dài là 10 m, chiều rộng là 8 m và chiều cao là 4 m. Một chiếc đèn được treo tại chính giữa trần nhà của phòng học. Xét hệ trục tọa độ Oxyz có gốc O trùng với một góc phòng và mặt phẳng (Oxy) trùng với mặt sàn, đơn vị đo được lấy theo mét.

Tính khoảng cách từ điểm treo bóng đèn đến góc phòng học (kết quả làm tròn đến hàng phần trăm). (ảnh 1)

Tính khoảng cách từ điểm treo bóng đèn đến góc phòng học (kết quả làm tròn đến hàng phần trăm).
A. 57;
B. 7,55;
C. 75,5;
D. 5,75.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Trong không gian với một hệ trục tọa độ Oxyz cho trước (đơn vị đo lấy theo mét), một công ty xây dựng cần xác định chiều dài của một sợi dây cáp nối giữa hai điểm cao trên hai toàn nhà để lắp đặt hệ thống điện. Tòa nhà thứ nhất có đỉnh ở vị trí A(3; 5; 12) và tòa nhà thứ hai có đỉnh ở vị trí B(8; 2; 20). Hỏi công ty cần chuẩn bị sợi dây cáp có chiều dài tối thiểu là bao nhiêu mét để nối hai đỉnh tòa nhà (làm tròn đến hàng đơn vị).
A. 12;
B. 11; 
C. 10;
D. 9.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Trong không gian chọn hệ trục tọa độ cho trước, đơn vị đo lấy theo km, một ra đa phát hiện một máy bay di chuyển với vận tốc và hướng không đổi từ điểm M(1000; 600; 14) đến điểm N(a; b; c) trong 30 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì sau 10 phút tiếp theo máy bay đến vị trí điểm Q(1400; 800; 18). Tính a + b + c.
A. 2760;
B. 2076; 
C. 2706;
D. 2067.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Một chiếc máy ảnh được đặt trên giá đỡ ba chân với điểm đặt E(0; 0; 8) và các điểm tiếp xúc với mặt đất của ba chân lần lượt là A1(0; 1; 0), \({A_2}\left( {\frac{{\sqrt 3 }}{2}; - \frac{1}{2};0} \right),{A_3}\left( {\frac{{ - \sqrt 3 }}{2}; - \frac{1}{2};0} \right)\).

Tọa độ của các lực tác dụng lên giá đỡ là (ảnh 1)
A. \(\overrightarrow {{F_1}} = \left( {0;10; - 80} \right)\);
B. \(\overrightarrow {{F_1}} = \left( {0;10;80} \right)\);
C. \(\overrightarrow {{F_1}} = \left( {0; - 10; - 80} \right)\);
D. \(\overrightarrow {{F_1}} = \left( {10;0; - 80} \right)\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Đăng ký

Bạn đã có tài khoản?

Khóa học 1 - 12
THPT
THCS
Phòng luyện đề
ĐGNL - ĐGTD
Tốt nghiệp THPT
Ôn vào 10
Ôn vào 6
Tài liệu
THPT
THCS
Tin Tuyển Sinh
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack72. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập