Trong không gian Oxyz, đường băng của một sân bay thuộc mặt phẳng (Oxy). Một máy bay sau khi chạy đà trên đường băng đó đã cất cánh tại điểm A(1; 2; 0) với vận tốc không đổi trong khoảng thời gian ngắn ban đầu, vectơ vận tốc \(\overrightarrow v = \left( {0;\sqrt 3 ;1} \right)\). Trong khoảng thời gian ngắn nói trên, góc cất cánh của máy bày bằng.

A. 90°;

B. 60°;

C. 30°;

D. 45°.

Câu hỏi trong đề: 10 bài tập Vận dụng công thức tính góc trong không gian vào giải quyết bài toán liên quan thực tế có lời giải !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đáp án đúng là: C

Trong khoảng thời gian ngắn đó, máy bay chuyển động trên đường thẳng đi qua A nhận \(\overrightarrow v = \left( {0;\sqrt 3 ;1} \right)\) làm vectơ chỉ phương.

Mặt phẳng (Oxy) có một vectơ pháp tuyến là \(\overrightarrow k = \left( {0;0;1} \right)\).

Ta có \(\sin \left( {\Delta ,\left( {Oxy} \right)} \right) = \frac{{\left| {\overrightarrow v .\overrightarrow k } \right|}}{{\left| {\overrightarrow v } \right|.\left| {\overrightarrow k } \right|}} = \frac{1}{2}\) (, (Oxy)) = 30°.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Khi gắn hệ trục tọa độ Oxyz (đơn vị trên mỗi trục tính theo mét) vào một căn nhà sao cho nền nhà thuộc mặt phẳng (Oxy), người ta coi mỗi mái nhà là một phần của mặt phẳng và thấy ba vị trí A, B, C ở mái nhà bên phải lần lượt có tọa độ (1; 0; 3), (5; 0; 1), (5; 9; 1). Góc giữa mái nhà bên phải và nền nhà bằng bao nhiêu độ (làm tròn kết quả đến hàng đơn vị)?

A. 72°;

B. 37°;

C. 73°;

D. 27°.

Lời giải

Đáp án đúng là: D

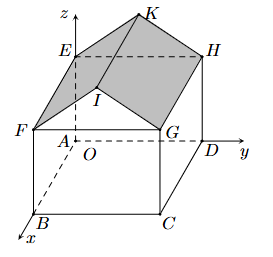
Mặt phẳng (ABC) có cặp vectơ chỉ phương là \(\overrightarrow {AB} = \left( {4;0; - 2} \right),\overrightarrow {BC} = \left( {0;9;0} \right)\).

Ta có \(\left[ {\overrightarrow {AB} ,\overrightarrow {BC} } \right] = \left( {18;0;36} \right)\).

Do đó vectơ pháp tuyến của mặt phẳng (ABC) là \(\overrightarrow {{n_1}} = \left( {1;0;2} \right)\).

Lại có, (Oxy) có vectơ pháp tuyến là \(\overrightarrow {{n_2}} = \left( {0;0;1} \right)\).

Ta có góc α là góc giữa mái nhà bên phải và nên nhà. Khi đó:

\(\cos \alpha = \frac{{\left| {1.0 + 0.0 + 2.1} \right|}}{{\sqrt {{1^2} + {2^2}} .\sqrt {{1^2}} }} = \frac{2}{{\sqrt 5 }}\) α ≈ 27°.

Câu 2

Trong không gian với hệ tọa độ Oxyz, một cabin cáp treo xuất phát từ điểm A(10; 3; 0) và chuyển động đều theo đường cáp có vectơ chỉ phương là \(\overrightarrow u = \left( {2; - 2;1} \right)\) với tốc độ là 4,5 m/s (đơn vị trên mỗi trục tọa độ là mét). Cabin dừng ở điểm B. Đường cáp AB tạo với mặt phẳng (Oxy) một góc bao nhiêu độ (làm tròn kết quả đến hàng đơn vị của độ)?

A. 19°;

B. 20°;

C. 21°;

D. 22°.

Lời giải

Đáp án đúng là: A

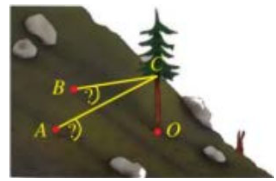
Đường thẳng AB có một vectơ chỉ phương \(\overrightarrow u = \left( {2; - 2;1} \right)\) và (Oxy) có một vectơ pháp tuyến \(\overrightarrow k = \left( {0;0;1} \right)\).

Do đó \(\sin \left( {AB,\left( {Oxy} \right)} \right) = \frac{{\left| {2.0 + \left( { - 2} \right).0 + 1.1} \right|}}{{\sqrt {{2^2} + {{\left( { - 2} \right)}^2} + {1^2}} .\sqrt {{1^2}} }} = \frac{1}{3}\) (AB, (Oxy)) ≈ 19°.

Câu 3