Câu hỏi:
19/05/2025 12
Ngày Hạ Chí chỉ khoảng thời gian bắt đầu mùa hè tại Bắc bán cầu và mùa đông ở Nam bán cầu. Hiện tượng này xảy ra khi một trong hai cực của Trái Đất có độ nghiêng tối đa về phía Mặt Trời. Vào ngày hạ chí, Trái Đất sẽ nhận lượng bức xạ lớn, thời gian ngày dài hơn đêm, trời lâu tối và nhanh sáng. Thậm chí, một số thành phố ở Bắc Âu còn có hiện tượng đêm trắng, tức là hoàn toàn không có ban đêm. Số giờ có ánh sáng của thành phố \(A\) trong ngày thứ \(t\) của một năm không nhuận được cho bởi hàm số \(d\left( t \right){\kern 1pt} \, = \,3\sin \left[ {\frac{\pi }{{182}}\left( {t - 180} \right) + 12} \right]\) với \(t \in \mathbb{Z}\) và \(0 < t \le 365\). Bạn An đến thành phố \(A\)và được biết hôm ấy là ngày Hạ Chí, ngày có nhiều ánh sáng mặt trời nhất trong năm của thành phố đó. Hỏi An đến thành phố \(A\) vào ngày nào trong năm?
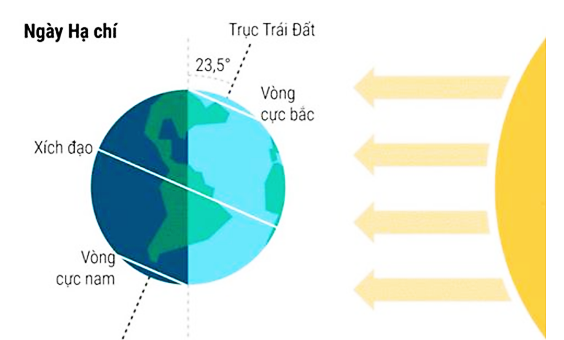
Ngày Hạ Chí chỉ khoảng thời gian bắt đầu mùa hè tại Bắc bán cầu và mùa đông ở Nam bán cầu. Hiện tượng này xảy ra khi một trong hai cực của Trái Đất có độ nghiêng tối đa về phía Mặt Trời. Vào ngày hạ chí, Trái Đất sẽ nhận lượng bức xạ lớn, thời gian ngày dài hơn đêm, trời lâu tối và nhanh sáng. Thậm chí, một số thành phố ở Bắc Âu còn có hiện tượng đêm trắng, tức là hoàn toàn không có ban đêm. Số giờ có ánh sáng của thành phố \(A\) trong ngày thứ \(t\) của một năm không nhuận được cho bởi hàm số \(d\left( t \right){\kern 1pt} \, = \,3\sin \left[ {\frac{\pi }{{182}}\left( {t - 180} \right) + 12} \right]\) với \(t \in \mathbb{Z}\) và \(0 < t \le 365\). Bạn An đến thành phố \(A\)và được biết hôm ấy là ngày Hạ Chí, ngày có nhiều ánh sáng mặt trời nhất trong năm của thành phố đó. Hỏi An đến thành phố \(A\) vào ngày nào trong năm?
Câu hỏi trong đề: 22 bài tập Bài tập cuối Chương I có lời giải !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có \(d{\left( t \right)_{\max }} \Leftrightarrow \sin \left[ {\frac{\pi }{{182}}\left( {t - 80} \right)} \right] = 1 \Leftrightarrow \frac{\pi }{{182}}\left( {t - 80} \right) = \frac{\pi }{2} + k2\pi \Leftrightarrow t = 171 + 364k\,\,\left( {k \in \mathbb{Z}} \right)\).
Vì \(0 < t \le 365\)và \(k \in \mathbb{Z}\) nên \(t = 171\).
Vậy An đến thành phố A vào ngày thứ 171 của năm.
Đáp án: 171.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8
Đã bán 211
₫ 119.000
₫ 45.000
Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025
Đã bán 244
₫ 136.000
₫ 58.000
Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack
Đã bán 1k
₫ 104.000
₫ 52.000
Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack
Đã bán 218
₫ 130.000
₫ 75.000
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Nếu \(\sin \alpha .\cos \left( {\alpha + \beta } \right) = \sin \beta \) với \(\alpha + \beta \ne \frac{\pi }{2} + k\pi ,\,\,\alpha \ne \frac{\pi }{2} + l\pi ,\,\,\left( {k,\,l \in \mathbb{Z}} \right)\) thì
Xem đáp án »
19/05/2025
18
Câu 2:
Cho phương trình \(\sin \left( {2x - \frac{\pi }{4}} \right) = \sin \left( {x + \frac{{3\pi }}{4}} \right)\) (*).
a) Phương trình có nghiệm: \(x = \pi + k2\pi \) và \(x = \frac{\pi }{6} + k\frac{{2\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right)\).
b) Trong khoảng \(\left( {0;\pi } \right)\), phương trình có 2 nghiệm.
c) Tổng các nghiệm của phương trình trong khoảng \(\left( {0;\pi } \right)\) bằng \(\frac{{7\pi }}{6}\).
d) Trong khoảng \(\left( {0;\pi } \right)\), phương trình có nghiệm lớn nhất bằng \(\frac{{5\pi }}{6}\).
Cho phương trình \(\sin \left( {2x - \frac{\pi }{4}} \right) = \sin \left( {x + \frac{{3\pi }}{4}} \right)\) (*).
a) Phương trình có nghiệm: \(x = \pi + k2\pi \) và \(x = \frac{\pi }{6} + k\frac{{2\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right)\).
b) Trong khoảng \(\left( {0;\pi } \right)\), phương trình có 2 nghiệm.
c) Tổng các nghiệm của phương trình trong khoảng \(\left( {0;\pi } \right)\) bằng \(\frac{{7\pi }}{6}\).
d) Trong khoảng \(\left( {0;\pi } \right)\), phương trình có nghiệm lớn nhất bằng \(\frac{{5\pi }}{6}\).
Xem đáp án »
19/05/2025
18
Câu 3:
Cho tam giác \(ABC\) có ba góc \(A\),\(B\),\(C\) thỏa mãn \(\sin A = \cos B + \cos C\)
a) Tam giác \(ABC\) có \(\frac{{B + C}}{2} = \frac{\pi }{2} - \frac{A}{2}\).
b) \(\cos \frac{{B + C}}{2} = \cos \frac{A}{2}\).
c) \(\sin A = \cos B + \cos C \Leftrightarrow \cos \frac{A}{2} = \cos \frac{{B - C}}{2}\).
d) Tam giác \(ABC\) là tam giác cân.
Cho tam giác \(ABC\) có ba góc \(A\),\(B\),\(C\) thỏa mãn \(\sin A = \cos B + \cos C\)
a) Tam giác \(ABC\) có \(\frac{{B + C}}{2} = \frac{\pi }{2} - \frac{A}{2}\).
b) \(\cos \frac{{B + C}}{2} = \cos \frac{A}{2}\).
c) \(\sin A = \cos B + \cos C \Leftrightarrow \cos \frac{A}{2} = \cos \frac{{B - C}}{2}\).
d) Tam giác \(ABC\) là tam giác cân.
Xem đáp án »
19/05/2025
17
Câu 4:
Cho phương trình lượng giác \(\cot 3x = - \frac{1}{{\sqrt 3 }}\) (*).
a) Phương trình (*) tương đương \(\cot 3x = \cot \left( {\frac{{ - \pi }}{6}} \right)\).
b) Phương trình (*) có nghiệm \(x = \frac{\pi }{9} + k\frac{\pi }{3}\,\,\left( {k \in \mathbb{Z}} \right)\).
c) Tổng các nghiệm của phương trình trong khoảng \(\left( { - \frac{\pi }{2};0} \right)\) bằng \(\frac{{ - 5\pi }}{9}\).
d) Phương trình có nghiệm dương nhỏ nhất bằng \(\frac{{2\pi }}{9}\).
Cho phương trình lượng giác \(\cot 3x = - \frac{1}{{\sqrt 3 }}\) (*).
a) Phương trình (*) tương đương \(\cot 3x = \cot \left( {\frac{{ - \pi }}{6}} \right)\).
b) Phương trình (*) có nghiệm \(x = \frac{\pi }{9} + k\frac{\pi }{3}\,\,\left( {k \in \mathbb{Z}} \right)\).
c) Tổng các nghiệm của phương trình trong khoảng \(\left( { - \frac{\pi }{2};0} \right)\) bằng \(\frac{{ - 5\pi }}{9}\).
d) Phương trình có nghiệm dương nhỏ nhất bằng \(\frac{{2\pi }}{9}\).
Xem đáp án »
19/05/2025
16
Câu 5:
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Khẳng định nào sau đây là đúng?
PHẦN I. TRẮC NGHIỆM NHIỀU LỰA CHỌN
Khẳng định nào sau đây là đúng?
Xem đáp án »
19/05/2025
15
Câu 6:
Một vật dao động xung quanh vị trí cân bằng theo phương trình \(x = 1,5\cos \left( {\frac{{t\pi }}{4}} \right)\); trong đó \(t\) là thời gian được tính bằng giây và quãng đường \(h = \left| x \right|\) được tính bằng mét là khoảng cách theo phương ngang của chất điểm đối với vị trí cân bằng (xem hình bên).
a) Vật ở xa vị trí cân bằng nhất nghĩa là \(h = 1,5\;\,{\rm{m}}\).
b) Trong 10 giây đầu tiên, có hai thời điểm vật ở xa vị trí cân bằng nhất.
c) Khi vật ở vị trí cân bằng thì \(\cos \left( {\frac{{t\pi }}{4}} \right) = 0\).
d) Trong khoảng từ 0 đến 20 giây thì vật đi qua vị trí cân bằng 4 lần.
a) Vật ở xa vị trí cân bằng nhất nghĩa là \(h = 1,5\;\,{\rm{m}}\).
b) Trong 10 giây đầu tiên, có hai thời điểm vật ở xa vị trí cân bằng nhất.
c) Khi vật ở vị trí cân bằng thì \(\cos \left( {\frac{{t\pi }}{4}} \right) = 0\).
d) Trong khoảng từ 0 đến 20 giây thì vật đi qua vị trí cân bằng 4 lần.
Xem đáp án »
19/05/2025
14
Câu 7:
Cho \[2\tan a - \cot a = 1\] với \[ - \frac{\pi }{2} < a < 0\]. Tính giá trị biểu thức \[P = \frac{{\tan \left( {6\pi - a} \right) - 2\cot \left( {3\pi + a} \right)}}{{3\tan \left( {\frac{{3\pi }}{2} + a} \right)}}\] (viết kết quả dưới dạng số thập phân).
Cho \[2\tan a - \cot a = 1\] với \[ - \frac{\pi }{2} < a < 0\]. Tính giá trị biểu thức \[P = \frac{{\tan \left( {6\pi - a} \right) - 2\cot \left( {3\pi + a} \right)}}{{3\tan \left( {\frac{{3\pi }}{2} + a} \right)}}\] (viết kết quả dưới dạng số thập phân).
Xem đáp án »
19/05/2025
14
🔥 Đề thi HOT:
-
10 Bài tập Nhận biết góc phẳng của góc nhị diện và tính góc phẳng nhị diện (có lời giải)
-
Bài tập Hình học không gian lớp 11 cơ bản, nâng cao có lời giải (P11)
-
10 Bài tập Biến cố hợp. Biến cố giao (có lời giải)
-
Bài tập Xác suất ôn thi THPT Quốc gia có lời giải (P1)
-
15 câu Trắc nghiệm Khoảng cách có đáp án (Nhận biết)
-
10 Bài tập Nhận biết góc phẳng của góc nhị diện và tính góc phẳng nhị diện (có lời giải)
-
10 Bài tập Bài toán thực tiễn liên quan đến thể tích (có lời giải)
-
23 câu Trắc nghiệm Xác suất của biến cố có đáp án (Phần 2)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận