Câu hỏi:
23/05/2025 308
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(y = \frac{{{x^2} + 3x + 3}}{{x + 2}}\) có đồ thị là \(\left( C \right)\) và hai điểm \(A,B\) là hai điểm cực trị của \(\left( C \right)\).
a) Đạo hàm của hàm số đã cho là \(y' = \frac{{{x^2} + 4x + 3}}{{{{\left( {x + 2} \right)}^2}}}\).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(y = \frac{{{x^2} + 3x + 3}}{{x + 2}}\) có đồ thị là \(\left( C \right)\) và hai điểm \(A,B\) là hai điểm cực trị của \(\left( C \right)\).
a) Đạo hàm của hàm số đã cho là \(y' = \frac{{{x^2} + 4x + 3}}{{{{\left( {x + 2} \right)}^2}}}\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Đúng. Điều kiện: \(x + 2 \ne 0 \Leftrightarrow x \ne - 2\) nên tập xác định của hàm số là \(D = \mathbb{R}\backslash \left\{ { - 2} \right\}\).
Ta có \(y' = \frac{{\left( {2x + 3} \right)\left( {x + 2} \right) - \left( {{x^2} + 3x + 3} \right)}}{{{{\left( {x + 2} \right)}^2}}} = \frac{{{x^2} + 4x + 3}}{{{{\left( {x + 2} \right)}^2}}}\).
Câu hỏi cùng đoạn
Câu 2:
b) Đường thẳng \(AB\) có phương trình là \(y = 2x + 1\).
b) Đường thẳng \(AB\) có phương trình là \(y = 2x + 1\).
Lời giải của GV VietJack
b) Sai. Cho \(y' = 0 \Leftrightarrow {x^2} + 4x + 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1 \Rightarrow y = 1\\x = - 3 \Rightarrow y = - 3\end{array} \right.\).
Do đó \(A\left( { - 1\,;1} \right),\,B\left( { - 3\,; - 3} \right)\) là hai điểm cực trị của hàm số.
Ta có \(\overrightarrow {AB} = \left( { - 2; - 4} \right)\), khi đó đường thẳng \(AB\) có phương trình là:
\(2\left( {x + 1} \right) - \left( {y - 1} \right) = 0 \Leftrightarrow y = 2x + 3\).
Câu 3:
c) Hai điểm \(A\) và \(B\) nằm ở hai phía trục tung.
c) Hai điểm \(A\) và \(B\) nằm ở hai phía trục tung.
Lời giải của GV VietJack
c) Sai. Vì \(A\left( { - 1\,;1} \right),\,B\left( { - 3\,; - 3} \right)\) nên \({x_A}\) và \({x_B}\) cùng dấu, đồng thời có hoành độ âm.
Do đó hai điểm \(A\left( { - 1\,;1} \right),\,B\left( { - 3\,; - 3} \right)\) nằm về một phía trục tung.
Câu 4:
d) Hai điểm \(A,B\) đối xứng nhau qua đường thẳng \(\Delta \) có phương trình \(x + 2y + 4 = 0\).
d) Hai điểm \(A,B\) đối xứng nhau qua đường thẳng \(\Delta \) có phương trình \(x + 2y + 4 = 0\).
Lời giải của GV VietJack
d) Đúng. Gọi \(I\) là trung điểm \(AB\) nên \(I\left( { - 2; - 1} \right)\).
Thay toạ độ \(I\left( { - 2; - 1} \right)\) vào đường thẳng \(\Delta :x + 2y + 4 = 0\) ta thấy thoả mãn nên \(I \in \Delta \).
Lại có \({\vec u_\Delta } \cdot \overrightarrow {AB} = 2 \cdot \left( { - 2} \right) + \left( { - 4} \right) \cdot \left( { - 1} \right) = 0\) nên \[\Delta \bot AB\].
Vậy hai điểm điểm \(A,B\) đối xứng nhau qua đường thẳng \(\Delta \).
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Đúng. Xác suất để cả 3 sinh viên đều dùng cà phê để duy trì tỉnh táo là \(0,{7^3} = 0,343\).
Lời giải
Đáp án: 2189.
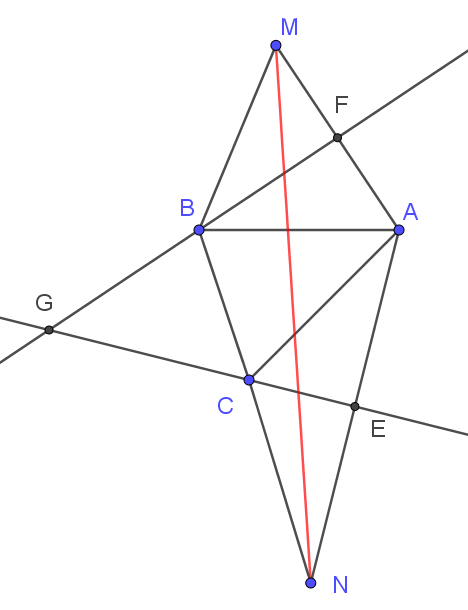
Do \({d_1} \cap {d_2} = G\left( { - 6;17;0} \right)\)\( \Rightarrow \left( {{d_1};{d_2}} \right) = \left( P \right):{\rm{ }}z = 0\).
+ \(M\)đối xứng với \(A\) qua \({d_1}\)
mp\(\left( Q \right)\) qua điểm \(A\) và vuông góc với \({d_1}\) có phương trình: \(x - 2y - 5 = 0\)
\(F = \left( Q \right) \cap {d_1} \Rightarrow F\left( {3; - 1;0} \right)\)
\(M\)đối xứng với \(A\) qua \({d_1}\)\( \Rightarrow F\)là trung điểm \(AM \Rightarrow M\left( {1; - 2;0} \right)\).
+ \(N\)đối xứng với \(A\) qua \({d_1}\)
mp\(\left( R \right)\) qua điểm \(A\) và vuông góc với \({d_2}\) có phương trình: \(x - y - 5 = 0\)
\(E = \left( R \right) \cap {d_2} \Rightarrow E\left( {8;3;0} \right)\)
\(N\)đối xứng với \(A\) qua \({d_2}\)\( \Rightarrow E\)là trung điểm \(AN \Rightarrow N\left( {11;6;0} \right)\)
+ Ta có \(P = AB + BC + CA = BM + BC + CN \ge MN\).
Suy ra \({P_{\min }} = MN = \sqrt {{{\left( {11 - 1} \right)}^2} + {{\left( {6 + 2} \right)}^2}} = \sqrt {164} \).
Vậy \(a + 2025 = 164 + 2025 = 2189\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
30 Đề thi thử thpt quốc gia môn Toán có lời giải chi tiết mới nhất (Đề số 1)
-
CÂU TRẮC NGHIỆM ĐÚNG SAI
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 2)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 19)
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 2)
-
45 bài tập Xác suất có lời giải