Câu hỏi:
23/05/2025 719
Hai chiếc flycam được điều khiển cùng bay lên tại một địa điểm.
Sau một thời gian bay, chiếc flycam thứ nhất bay đến vị trí điểm \(A\) cách mặt đất \(10\,{\rm{m}}\), cách điểm xuất phát \(8\,{\rm{m}}\) về phía nam và \(3\,{\rm{m}}\) về phía đông. Chiếc flycam thứ hai bay đến điểm \(B\) cách mặt đất \(12\,{\rm{m}}\), cách điểm xuất phát \(4\,{\rm{m}}\) về phía bắc và \(5\,{\rm{m}}\) về phía tây. Chọn hệ trục tọa độ \(Oxyz\) với gốc \(O\) đặt tại điểm xuất phát của hai chiếc flycam, mặt phẳng \(\left( {Oxy} \right)\) trùng với mặt đất (coi như phẳng) có trục \(Ox\) hướng về phía nam, trục \(Oy\) hướng về phía đông và trục \(Oz\) hướng thẳng đứng lên trời (đơn vị đo trên mỗi trục là mét).
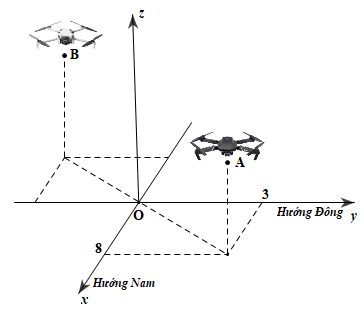
a) Tọa độ của điểm \(A\left( {8;\,3;\,10} \right)\).
Hai chiếc flycam được điều khiển cùng bay lên tại một địa điểm.
Sau một thời gian bay, chiếc flycam thứ nhất bay đến vị trí điểm \(A\) cách mặt đất \(10\,{\rm{m}}\), cách điểm xuất phát \(8\,{\rm{m}}\) về phía nam và \(3\,{\rm{m}}\) về phía đông. Chiếc flycam thứ hai bay đến điểm \(B\) cách mặt đất \(12\,{\rm{m}}\), cách điểm xuất phát \(4\,{\rm{m}}\) về phía bắc và \(5\,{\rm{m}}\) về phía tây. Chọn hệ trục tọa độ \(Oxyz\) với gốc \(O\) đặt tại điểm xuất phát của hai chiếc flycam, mặt phẳng \(\left( {Oxy} \right)\) trùng với mặt đất (coi như phẳng) có trục \(Ox\) hướng về phía nam, trục \(Oy\) hướng về phía đông và trục \(Oz\) hướng thẳng đứng lên trời (đơn vị đo trên mỗi trục là mét).
a) Tọa độ của điểm \(A\left( {8;\,3;\,10} \right)\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Đúng. Tọa độ của điểm \(A\left( {8;\,3;\,10} \right)\).
Câu hỏi cùng đoạn
Câu 2:
b) Phương trình đường thẳng đi qua vị trí của hai chiếc flycam tại \(A\) và \(B\) là \(\left\{ \begin{array}{l}x = 8 + 12t\\y = 3 + 8t\\z = 10 - 2t\end{array} \right.\).
b) Phương trình đường thẳng đi qua vị trí của hai chiếc flycam tại \(A\) và \(B\) là \(\left\{ \begin{array}{l}x = 8 + 12t\\y = 3 + 8t\\z = 10 - 2t\end{array} \right.\).
Lời giải của GV VietJack
b) Đúng. Tọa độ điểm \(B\left( { - 4;\, - 5;\,12} \right)\), \(\overrightarrow {AB} = \left( { - 12;\, - 8;\,2} \right)\).
Phương trình đường thẳng đi qua vị trí của hai chiếc flycam tại \(A\) và \(B\) là \(\left\{ \begin{array}{l}x = 8 + 12t\\y = 3 + 8t\\z = 10 - 2t\end{array} \right.\).
Câu 3:
c) Mặt phẳng trung trực của đoạn thẳng \(AB\) đi qua \(M\left( {1;\,2;\, - 1} \right)\).
c) Mặt phẳng trung trực của đoạn thẳng \(AB\) đi qua \(M\left( {1;\,2;\, - 1} \right)\).
Lời giải của GV VietJack
c) Sai. Gọi \(I\) là trung điểm của\(AB\)\( \Rightarrow I\left( {2;\, - 1;\,11} \right)\).
Mặt phẳng trung trực của đoạn thẳng \(AB\) đi qua \(I\) và nhận \(\overrightarrow {AB} \) làm vectơ pháp tuyến có dạng:
\( - 12\left( {x - 2} \right) - 8\left( {y + 1} \right) + 2\left( {z - 11} \right) = 0 \Leftrightarrow 6x + 4y - z + 3 = 0\).
Thay tọa độ điểm \(M\) vào phương trình: \(6 \cdot 1 + 4 \cdot 2 - \left( { - 1} \right) + 3 = 18 \ne 0\).
Do đó điểm \(M\) không thuộc mặt phẳng trung trực của đoạn thẳng \(AB\).
Câu 4:
d) Trên mặt đất người ta đặt một thiết bị phá sóng flycam sao cho có thể phá sóng hai chiếc flycam tại hai vị trí \(A,\,\,B\) cùng một lúc. Tổng khoảng cách ngắn nhất từ thiết bị đó đến hai chiếc flycam tại hai vị trí \(A\) và \(B\) (làm tròn kết quả đến hàng phần trăm) bằng \(25,46\,\,{\rm{(m)}}\).
d) Trên mặt đất người ta đặt một thiết bị phá sóng flycam sao cho có thể phá sóng hai chiếc flycam tại hai vị trí \(A,\,\,B\) cùng một lúc. Tổng khoảng cách ngắn nhất từ thiết bị đó đến hai chiếc flycam tại hai vị trí \(A\) và \(B\) (làm tròn kết quả đến hàng phần trăm) bằng \(25,46\,\,{\rm{(m)}}\).
Lời giải của GV VietJack
d) Sai. Gọi \(N\) là vị trí đặt thiết bị phá sóng flycam. Vì thiết bị có thể phá sóng cùng lúc hai chiếc flycam nên \(NA = NB\).
Suy ra \(N\) thuộc mặt phẳng trung trực \(\left( P \right)\) của \(AB\).
\(N \in \left( {Oxy} \right) \Rightarrow N\) thuộc giao tuyến \(\Delta \) của \(\left( P \right)\) và \(\left( {Oxy} \right)\).
\(\Delta \) có một VTCP \(\overrightarrow {{u_\Delta }} = \left[ {\overrightarrow k ,\,\overrightarrow {{n_{\left( P \right)}}} } \right] = \left( { - 4;\,6;\,0} \right)\). Lấy \(I \in \Delta \Rightarrow \left\{ \begin{array}{l}I \in \left( {Oxy} \right)\\I \in \left( P \right)\end{array} \right. \Rightarrow I\left( { - \frac{1}{2};\,0;\,0} \right)\).
\( \Rightarrow \overrightarrow {IA} = \left( {\frac{{17}}{2};\,3;\,10} \right)\).
Ta có \(T = NA + NB = 2NA\).
\({T_{\min }} \Leftrightarrow N{A_{\min }} \Leftrightarrow N\) là hình chiếu của \(A\) xuống \(\Delta \), tức là \(NA = d\left( {A,\Delta } \right) = \frac{{\left| {\left[ {\overrightarrow {IA} ,\overrightarrow {{u_\Delta }} } \right]} \right|}}{{\left| {\overrightarrow {{u_\Delta }} } \right|}} \approx 13,2788\).
Vậy \({T_{\min }} = 2NA \approx 26,56\).
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Đúng. Xác suất để cả 3 sinh viên đều dùng cà phê để duy trì tỉnh táo là \(0,{7^3} = 0,343\).
Lời giải
Đáp án: 2189.
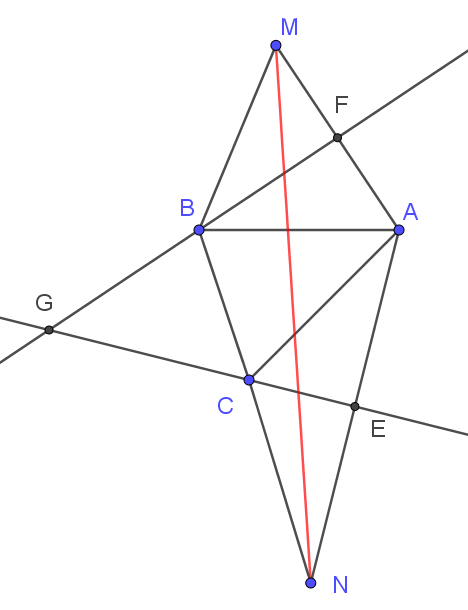
Do \({d_1} \cap {d_2} = G\left( { - 6;17;0} \right)\)\( \Rightarrow \left( {{d_1};{d_2}} \right) = \left( P \right):{\rm{ }}z = 0\).
+ \(M\)đối xứng với \(A\) qua \({d_1}\)
mp\(\left( Q \right)\) qua điểm \(A\) và vuông góc với \({d_1}\) có phương trình: \(x - 2y - 5 = 0\)
\(F = \left( Q \right) \cap {d_1} \Rightarrow F\left( {3; - 1;0} \right)\)
\(M\)đối xứng với \(A\) qua \({d_1}\)\( \Rightarrow F\)là trung điểm \(AM \Rightarrow M\left( {1; - 2;0} \right)\).
+ \(N\)đối xứng với \(A\) qua \({d_1}\)
mp\(\left( R \right)\) qua điểm \(A\) và vuông góc với \({d_2}\) có phương trình: \(x - y - 5 = 0\)
\(E = \left( R \right) \cap {d_2} \Rightarrow E\left( {8;3;0} \right)\)
\(N\)đối xứng với \(A\) qua \({d_2}\)\( \Rightarrow E\)là trung điểm \(AN \Rightarrow N\left( {11;6;0} \right)\)
+ Ta có \(P = AB + BC + CA = BM + BC + CN \ge MN\).
Suy ra \({P_{\min }} = MN = \sqrt {{{\left( {11 - 1} \right)}^2} + {{\left( {6 + 2} \right)}^2}} = \sqrt {164} \).
Vậy \(a + 2025 = 164 + 2025 = 2189\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
30 Đề thi thử thpt quốc gia môn Toán có lời giải chi tiết mới nhất (Đề số 1)
-
CÂU TRẮC NGHIỆM ĐÚNG SAI
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 2)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 19)
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 2)
-
45 bài tập Xác suất có lời giải