PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Một công ty trung bình bán được 600 chiếc máy lọc không khí mỗi tháng với giá 10 triệu đồng một chiếc. Một khảo sát cho thấy nếu giảm giá bán mỗi chiếc 400 nghìn đồng, thì số lượng bán ra tăng thêm khoảng 60 chiếc mỗi tháng. Gọi \(p\) (triệu đồng) là giá bán của mỗi máy, \(x\) là số máy bán ra. Khi đó, hàm cầu \(p = p\left( x \right)\) và hàm doanh thu là \(R\left( p \right) = px\). Hỏi công ty phải bán mỗi máy lọc không khí với số tiền bao nhiêu triệu đồng để doanh thu là lớn nhất?
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Một công ty trung bình bán được 600 chiếc máy lọc không khí mỗi tháng với giá 10 triệu đồng một chiếc. Một khảo sát cho thấy nếu giảm giá bán mỗi chiếc 400 nghìn đồng, thì số lượng bán ra tăng thêm khoảng 60 chiếc mỗi tháng. Gọi \(p\) (triệu đồng) là giá bán của mỗi máy, \(x\) là số máy bán ra. Khi đó, hàm cầu \(p = p\left( x \right)\) và hàm doanh thu là \(R\left( p \right) = px\). Hỏi công ty phải bán mỗi máy lọc không khí với số tiền bao nhiêu triệu đồng để doanh thu là lớn nhất?
Quảng cáo
Trả lời:
Đáp án: 7.
Theo giả thiết, tốc độ thay đổi của \(x\) tỉ lệ với tốc độ thay đổi của \[p\] nên hàm số \(p = p\left( x \right)\) là hàm số bậc nhất. Do đó, \(p\left( x \right) = ax + b\) \((a\) khác 0\()\).
Giá tiền \({p_1} = 10\) ứng với \({x_1} = 600\), giá tiền \({p_2} = 9,6\) ứng với \({x_2} = 600 + 60 = 660\).
Do đó, phương trình đường thẳng \(p\left( x \right) = ax + b\) đi qua hai điểm \(\left( {600\,;10} \right)\) và \(\left( {660\,;9,6} \right)\).
Ta có hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{10 = 600a + b}\\{9,6 = 660a + b}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = \frac{{ - 1}}{{150}}}\\{b = 14}\end{array}} \right.\) (thỏa mãn).
Vậy hàm cầu là \(p\left( x \right) = - \frac{1}{{150}}x + 14\).
Vì \(p = - \frac{1}{{150}}x + 14 \Rightarrow x = - 150p + 2100\) suy ra hàm doanh thu là:
\(R\left( p \right) = px = p\left( { - 150p + 2100} \right) = 150\left( { - {p^2} + 14p} \right)\).
Ta có \(R(p)\) lớn nhất \( \Leftrightarrow p = \frac{{ - B}}{{2A}} = 7\).
Vậy công ty phải bán mỗi máy lọc không khí với số tiền 7 triệu đồng để doanh thu là lớn nhất.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: 0,36.
Gọi biến cố \(A\): “Ít nhất một trong hai người đó gọi đúng số điện thoại đã quên mà không phải thử quá hai lần”.
Khi đó, biến cố \(\bar A\): “Cả hai người gọi thử cả 2 lần đều không đúng”.
Xác suất gọi sai cả 2 lần của mỗi người là \(\frac{9}{{10}} \cdot \frac{8}{9} = \frac{4}{5}\).
Hai người gọi điện là độc lập nên \[P\left( {\overline A } \right) = \frac{4}{5} \cdot \frac{4}{5} = \frac{{16}}{{25}}\].
Vậy \(P\left( A \right) = 1 - \frac{{16}}{{25}} = \frac{9}{{25}} = 0,36\).
Lời giải
Đáp án: 12,4.
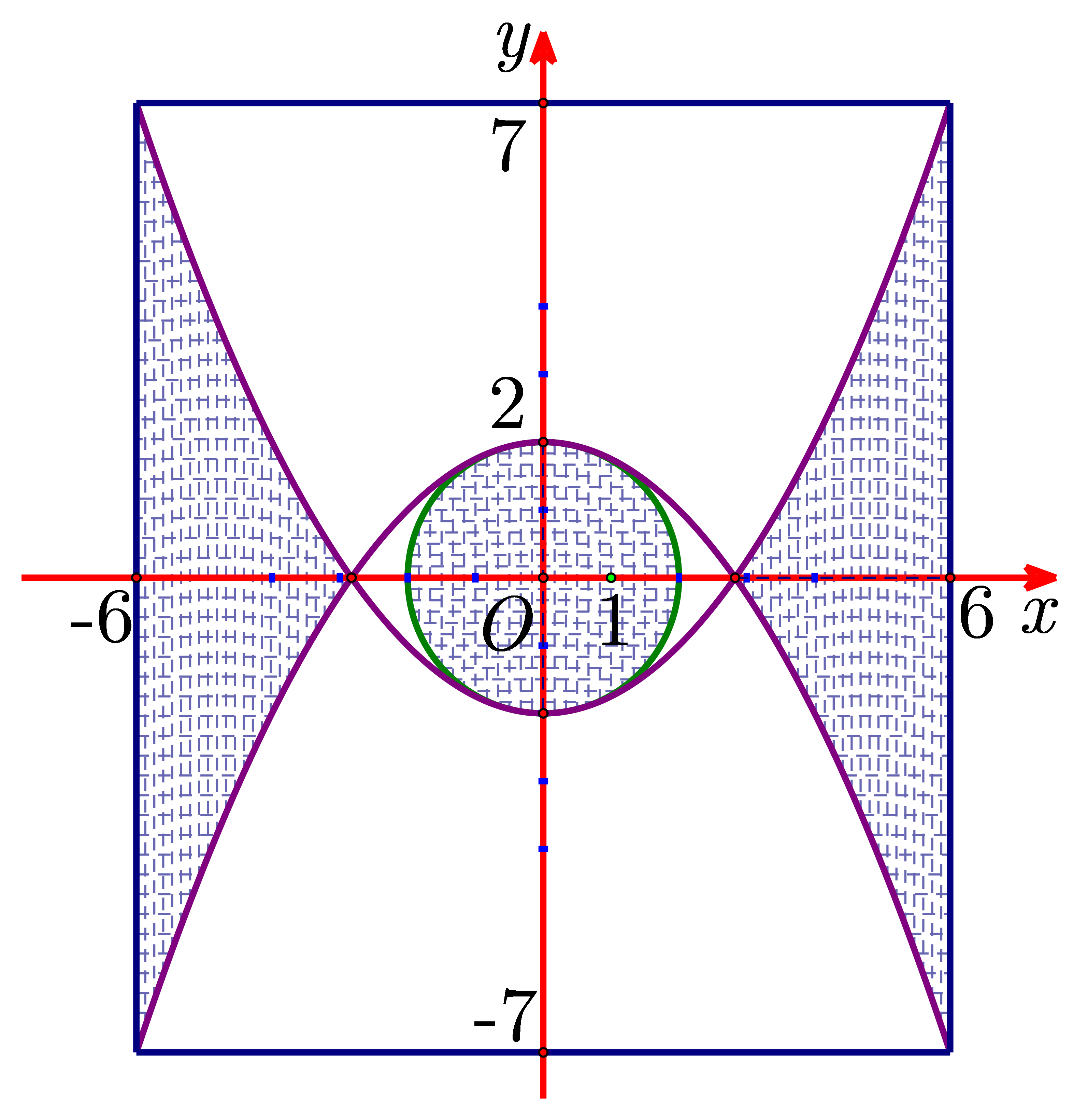
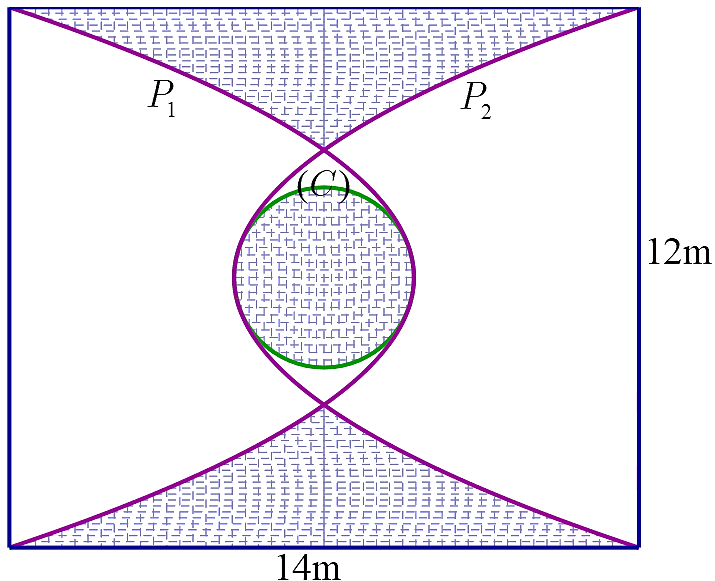
Chọn hệ trục tọa độ \(Oxy\) như hình vẽ với \(M\left( {0\,;\,m} \right)\,\,\left( {m < 0} \right)\) là đỉnh của parabol \(\left( {{P_1}} \right)\).
Khi đó \(\left( {{P_1}} \right):y = \frac{{7 - m}}{{36}}{x^2} + m\) và \(\left( C \right):{x^2} + {y^2} = {m^2}.\)
Để \(\left( {{P_1}} \right),\,\,\left( C \right)\) có một điểm chung duy nhất thì phương trình sau có nghiệm duy nhất.
\({x^2} + {\left( {\frac{{7 - m}}{{36}}{x^2} + m} \right)^2} = {m^2} \Leftrightarrow {x^2}\left[ {{{\left( {\frac{{7 - m}}{{36}}} \right)}^2}{x^2} + \frac{{ - {m^2} + 7m + 18}}{{18}}} \right] = 0\).
\({\rm{YCBT}} \Leftrightarrow - {m^2} + 7m + 18 \ge 0 \Leftrightarrow - 2 \le m \le 9\). Mà \(m < 0\) nên \( - 2 \le m < 0\).
Khi đó, đường tròn \(\left( C \right)\) có diện tích lớn nhất khi \(\left( C \right)\) có bán kính lớn nhất, điều này xảy ra khi và chỉ khi \(m = - 2 \Rightarrow r = 2.\)
Hoành độ giao điểm của \(\left( {{P_1}} \right):y = \frac{1}{4}{x^2} - 2\) và trục hoành là \(x = \pm 2\sqrt 2 \).
Diện tích phần lát gạch là \(S = 4\int\limits_{2\sqrt 2 }^6 {\left( {\frac{1}{4}{x^2} - 2} \right){\rm{d}}x} + \pi {r^2} = \frac{{72 + 32\sqrt 2 }}{3} + 4\pi \).
Số tiền lát gạch là: \(240S \approx 12396,32\) (nghìn đồng) \( \approx 12,4\) (triệu đồng).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.