Mẫu số liệu ghép nhóm thống kê mức lương của một công ty (đơn vị: triệu đồng) được cho trong bảng dưới đây.
Nhóm
(đơn vị: triệu đồng)
\[\left[ {6;8} \right)\]
\[\left[ {8;10} \right)\]
\[\left[ {10;12} \right)\]
\[\left[ {12;14} \right)\]
\[\left[ {14;16} \right)\]
Tần số
6
14
18
10
2
\[n = 50\]
Tứ phân vị thứ nhất của mẫu số liệu đã cho (làm tròn đến hàng phần trăm) là
Mẫu số liệu ghép nhóm thống kê mức lương của một công ty (đơn vị: triệu đồng) được cho trong bảng dưới đây.
|
Nhóm (đơn vị: triệu đồng) |
\[\left[ {6;8} \right)\] |
\[\left[ {8;10} \right)\] |
\[\left[ {10;12} \right)\] |
\[\left[ {12;14} \right)\] |
\[\left[ {14;16} \right)\] |
|
|
Tần số |
6 |
14 |
18 |
10 |
2 |
\[n = 50\] |
Quảng cáo
Trả lời:
Ta có \[\frac{n}{4} = \frac{{50}}{4} = 12,5 \Rightarrow {Q_1} \in \left[ {8;10} \right)\]. Khi đó \[{Q_1} = 8 + \frac{{12,5 - 6}}{{14}}.\left( {10 - 8} \right) \approx 8,93\]. Chọn D.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: 8.
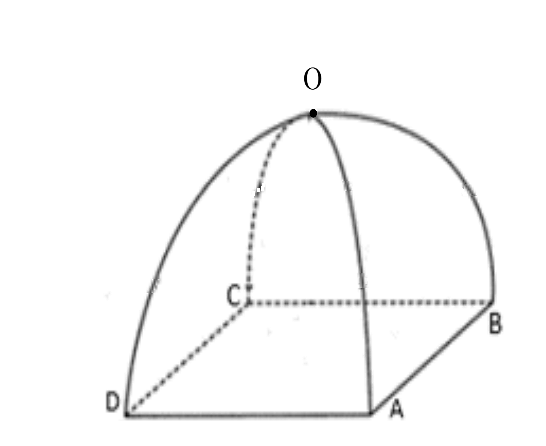
Ta có \(AB = 2\sqrt 2 \Rightarrow AC = 4.\) Chọn hệ trục \(Oxy\) như hình vẽ.
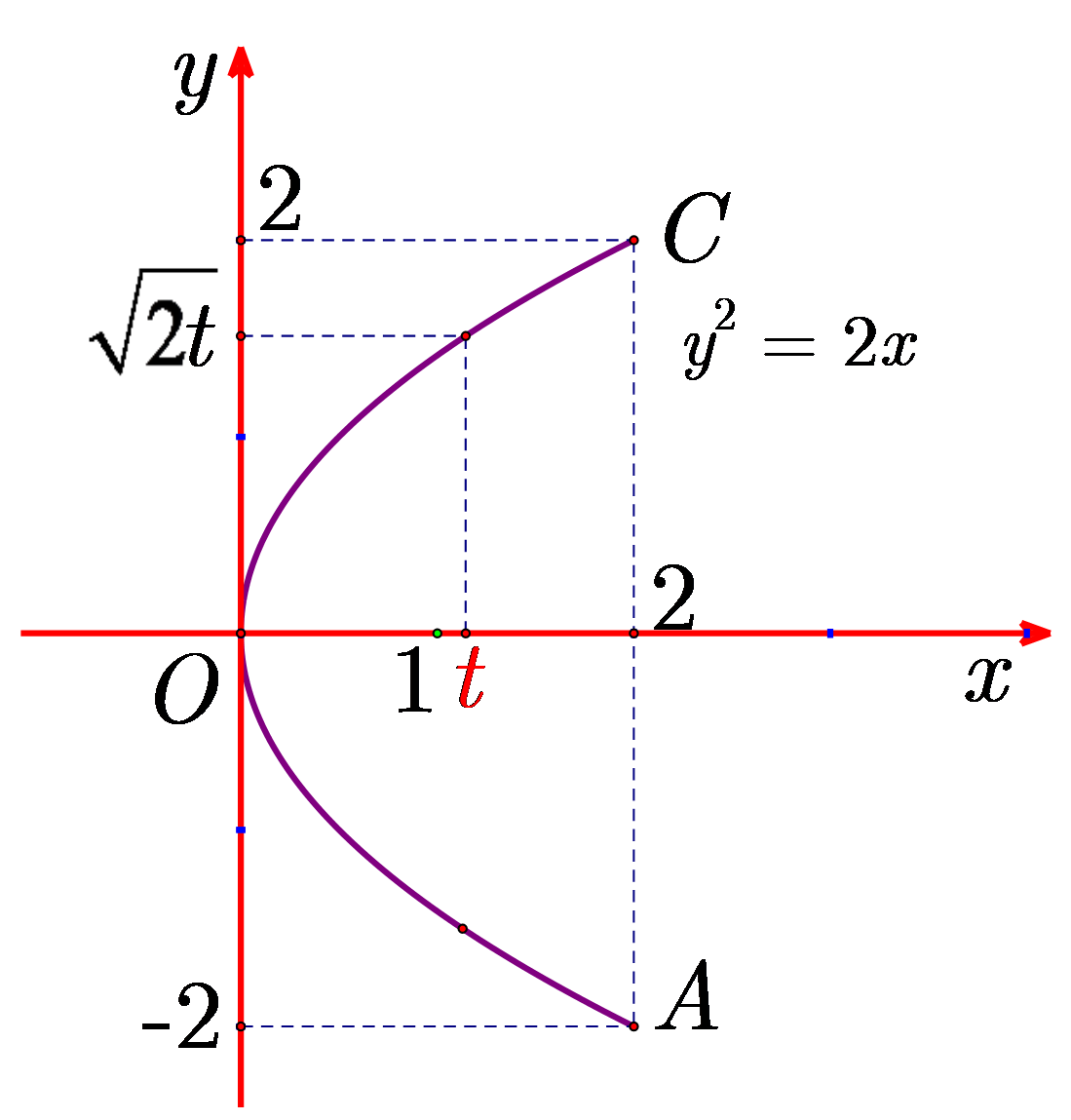
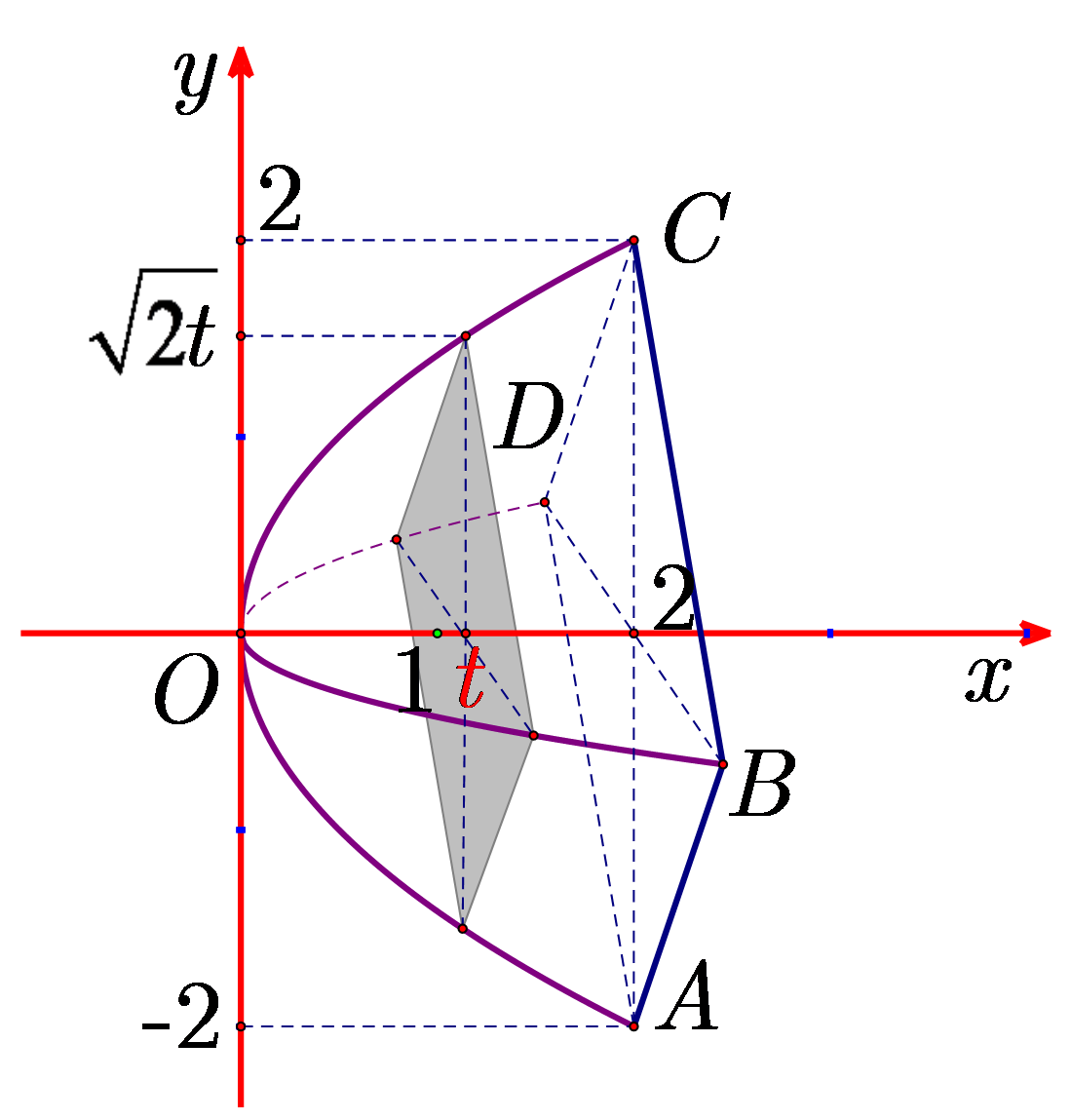
Khi đó, mặt cắt tại \(x = t\) là hình vuông có diện tích \(S\left( t \right) = \frac{1}{2}{\left( {2\sqrt {2t} } \right)^2} = 4t\).
Vậy thể tích của lều là \(V = \int\limits_0^2 {S\left( t \right){\rm{d}}t} = \int\limits_0^2 {4t{\rm{d}}t} = \left. {2{t^2}} \right|_0^2 = 8{\rm{ }}\left( {{{\rm{m}}^3}} \right).\)
Lời giải
Đáp án: 12.
Lợi nhận hộ thu được trong một ngày là
\(L\left( x \right) = 300x - \left( {\frac{{23}}{{36}}{x^3} + {x^2} + 200} \right) = - \frac{{23}}{{36}}{x^3} - {x^2} + 300x - 200\).
\(L'\left( x \right) = - \frac{{23}}{{36}} \cdot 3{x^2} - 2x + 300 = 0 \Leftrightarrow - \frac{{23}}{{12}}{x^2} - 2x + 300 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 12\,\,\,\,\,\,\,\,\,\left( {{\rm{tm}}} \right)\\x = - \frac{{300}}{{23}}\,\,\,\left( {\rm{L}} \right)\end{array} \right.\).
Ta có \(L\left( 1 \right) = \frac{{3541}}{{36}};\,\,L\left( {12} \right) = 2152;\,\,L\left( {20} \right) = \frac{{2600}}{9}\). Suy ra \(\mathop {\max }\limits_{\left[ {1\,;\,20} \right]} L\left( x \right) = L\left( {12} \right) = 2152\).
Vậy để lợi nhuận đạt tối đa thì mỗi ngày hộ cần sản xuất 12 mét vải lụa.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.