Câu hỏi:
23/05/2025 128
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và thoả mãn \(\int\limits_1^3 {f\left( x \right)} \,{\rm{d}}x = 2\).
a) \(\int\limits_1^3 {3f\left( x \right)} \,{\rm{d}}x = 6\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và thoả mãn \(\int\limits_1^3 {f\left( x \right)} \,{\rm{d}}x = 2\).
a) \(\int\limits_1^3 {3f\left( x \right)} \,{\rm{d}}x = 6\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Đúng. Ta có \(\int\limits_1^3 {3f\left( x \right)} \,{\rm{d}}x = 3\int\limits_1^3 {\left( x \right)} \,{\rm{d}}x = 3 \cdot 2 = 6\).
Câu hỏi cùng đoạn
Câu 2:
b) Nếu \(\int\limits_2^3 {f\left( x \right)} \,{\rm{d}}x = - 1\) thì \(\int\limits_1^2 {f\left( x \right)} \,{\rm{d}}x = 1\).
b) Nếu \(\int\limits_2^3 {f\left( x \right)} \,{\rm{d}}x = - 1\) thì \(\int\limits_1^2 {f\left( x \right)} \,{\rm{d}}x = 1\).
Lời giải của GV VietJack
b) Sai. Nếu \(\int\limits_2^3 {f\left( x \right)} \,{\rm{d}}x = - 1\) thì \(\int\limits_1^2 {f\left( x \right)} \,{\rm{d}}x = \int\limits_1^3 {f\left( x \right)} \,{\rm{d}}x - \int\limits_2^3 {f\left( x \right)} \,{\rm{d}}x = 2 - \left( { - 1} \right) = 3\).
Câu 3:
c) Nếu \(F\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\) trên đoạn \(\left[ {1;3} \right]\) thoả mãn \(F\left( 1 \right) = 3\) thì \(F\left( 3 \right) = 1\).
c) Nếu \(F\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\) trên đoạn \(\left[ {1;3} \right]\) thoả mãn \(F\left( 1 \right) = 3\) thì \(F\left( 3 \right) = 1\).
Lời giải của GV VietJack
c) Sai. Nếu \(F\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\) trên đoạn \(\left[ {1;3} \right]\) thoả mãn \(F\left( 1 \right) = 3\) thì
\(2 = \int\limits_1^3 {f\left( x \right)} \,{\rm{d}}x = F\left( 3 \right) - F\left( 1 \right) \Rightarrow F\left( 3 \right) = 2 + F\left( 1 \right) = 2 + 3 = 5\).
Câu 4:
d) \(\int\limits_1^3 {\frac{{xf\left( x \right) + {x^2} - 1}}{x}} \,{\rm{d}}x = a + b\ln 3\;\,\left( {a \in \mathbb{R},b \in \mathbb{R}} \right)\). Ta có \(a + b = 5\).
d) \(\int\limits_1^3 {\frac{{xf\left( x \right) + {x^2} - 1}}{x}} \,{\rm{d}}x = a + b\ln 3\;\,\left( {a \in \mathbb{R},b \in \mathbb{R}} \right)\). Ta có \(a + b = 5\).
Lời giải của GV VietJack
d) Đúng. Ta có \(\int\limits_1^3 {\frac{{xf\left( x \right) + {x^2} - 1}}{x}} \,{\rm{d}}x = \int\limits_1^3 {\left[ {f\left( x \right) + x - \frac{1}{x}} \right]} \,{\rm{d}}x = \int\limits_1^3 {f\left( x \right)} \,{\rm{d}}x + \int\limits_1^3 x {\rm{d}}x - \int\limits_1^3 {\frac{1}{x}} \,{\rm{d}}x\)
\( = 2 + \left. {\frac{{{x^2}}}{2}} \right|_1^3 - \left. {\ln \left| x \right|} \right|_1^3 = 2 + \frac{9}{2} - \frac{1}{2} - \ln 3 + \ln 1 = 6 - \ln 3 = a + b\ln 3\).
Suy ra \(a = 6;b = - 1 \Rightarrow a + b = 5\).
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: 8.
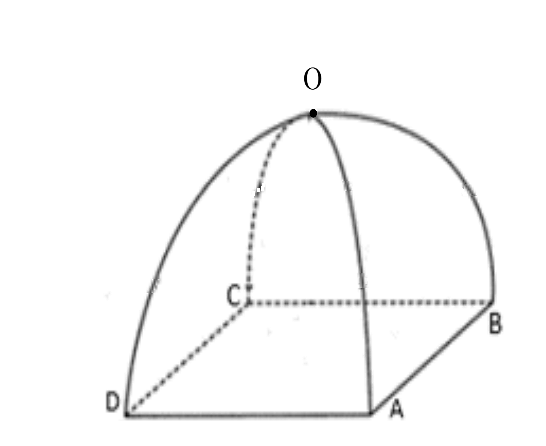
Ta có \(AB = 2\sqrt 2 \Rightarrow AC = 4.\) Chọn hệ trục \(Oxy\) như hình vẽ.
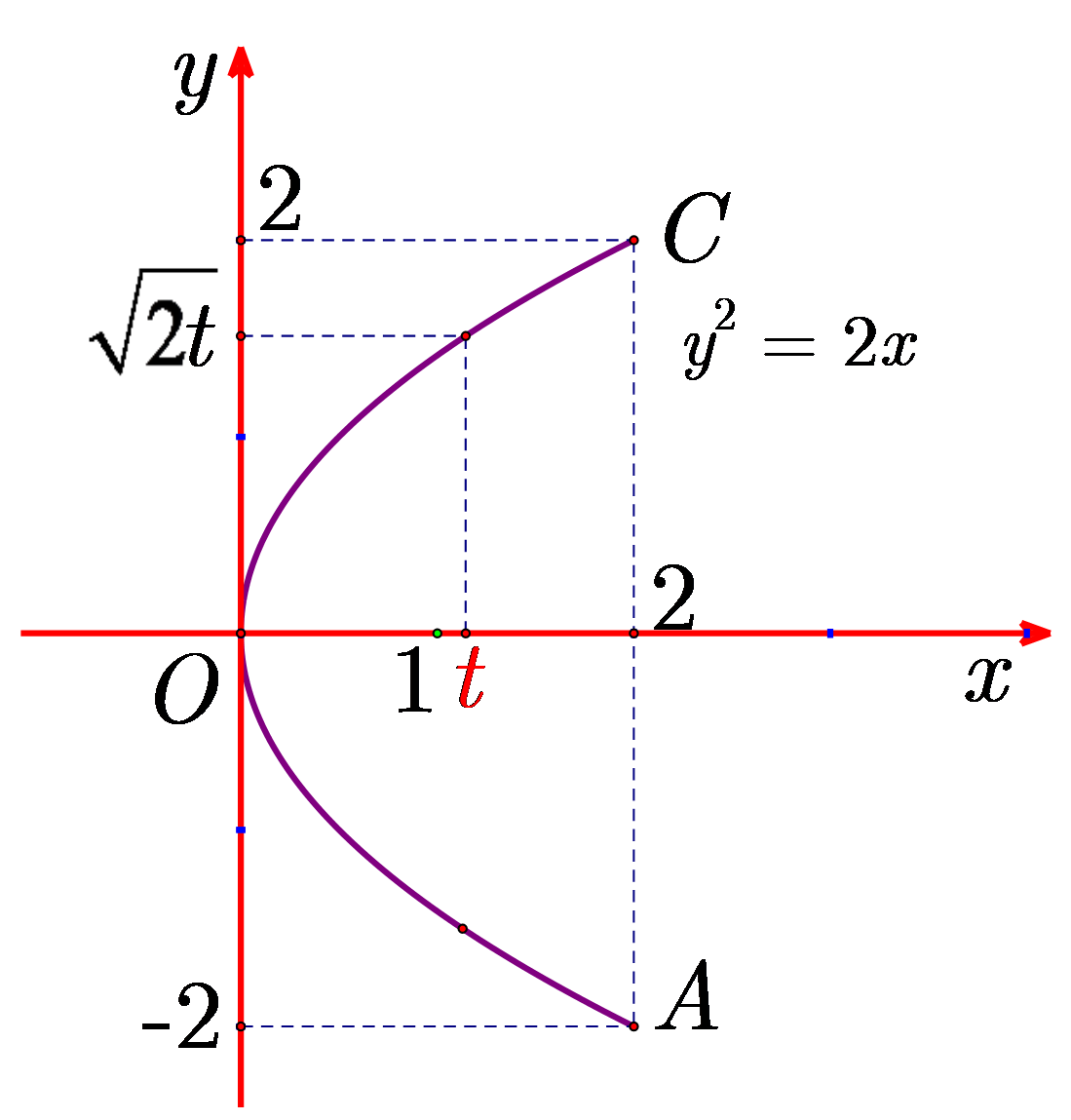
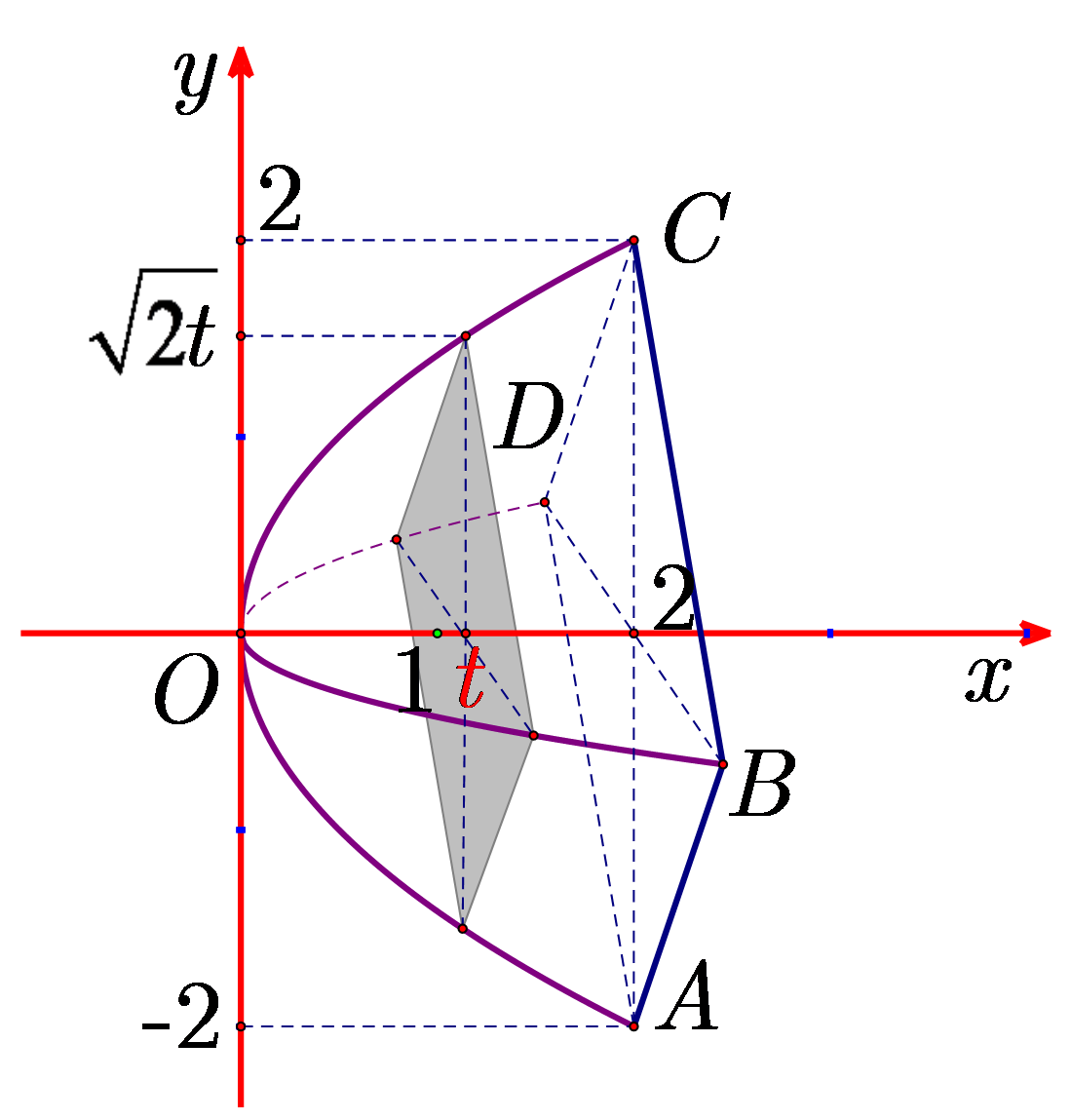
Khi đó, mặt cắt tại \(x = t\) là hình vuông có diện tích \(S\left( t \right) = \frac{1}{2}{\left( {2\sqrt {2t} } \right)^2} = 4t\).
Vậy thể tích của lều là \(V = \int\limits_0^2 {S\left( t \right){\rm{d}}t} = \int\limits_0^2 {4t{\rm{d}}t} = \left. {2{t^2}} \right|_0^2 = 8{\rm{ }}\left( {{{\rm{m}}^3}} \right).\)
Lời giải
Đáp án: 73,0.
Xác định các vectơ vận tốc:
Gọi \(\vec a:\) vectơ vận tốc của máy bay Su-30
\(\vec b:\) vectơ vận tốc của máy bay MiG-31
\(\vec c:\) vectơ vận tốc của gió
\({\vec u_1}:\) vectơ chỉ phương của đường thẳng quỹ đạo bay của máy bay Su-30
\({d_1}:\) đường thẳng quỹ đạo bay của máy bay Su-30
\({\vec u_2}:\) vectơ chỉ phương của đường thẳng quỹ đạo bay của máy bay MiG-31
\({d_2}:\) đường thẳng quỹ đạo bay của máy bay MiG-31
\(\left( T \right):\) mặt trụ có tâm \(C\left( {178\,;430\,;0} \right)\) bán kính \(r = 7.\)
\[\begin{array}{l}\left| {{{\vec v}_1}} \right| = \sqrt {{3^2} + {4^2} + {0^2}} = 5 \Rightarrow \vec a = \frac{{900}}{5}{{\vec v}_1} = \left( {540\,;720\,;0} \right)\\\left| {{{\vec v}_2}} \right| = 13 \Rightarrow \vec b = \frac{{910}}{{13}}{{\vec v}_2} = \left( {350\,;840\,;0} \right)\\\left| {\vec u} \right| = 5 \Rightarrow \vec c = \frac{{80}}{5}\vec u = \left( { - 48\,;0\,;64} \right)\\{{\vec u}_1} = \vec a + \vec c = \left( {492\,;720\,;64} \right) \Rightarrow {d_1}:\left\{ \begin{array}{l}x = 492t\\y = 35 + 720t\\z = 10 + 64t\end{array} \right.\\{{\vec u}_2} = \vec b + \vec c = \left( {302\,;840\,;64} \right) \Rightarrow {d_2}:\left\{ \begin{array}{l}x = 31 + 302t\\y = 10 + 840t\\z = 11 + 64t\end{array} \right.\\\left( T \right):{\left( {x - 178} \right)^2} + {\left( {y - 430} \right)^2} = {7^2}.\end{array}\]
Vì không phận cấm bay có độ cao \(43{\rm{ km}}\) nên MiG-31 vào trong không phận thì độ cao tối đa của máy bay là \(z \le 43 \Rightarrow 11 + 64t \le 43 \Leftrightarrow t \le 0,5.\)
Tìm giao điểm của \({d_2}\) và \(\left( T \right)\).
Xét phương trình: \({\left( {31 + 302t - 178} \right)^2} + {\left( {10 + 840t - 430} \right)^2} = 49\)
\( \Leftrightarrow 796804{t^2} - 794388t + 197960 = 0 \Leftrightarrow \left[ \begin{array}{l}t = 0,51 > 5\\t = 0,49 < 5\end{array} \right.\).
Dễ dàng nhận thấy MiG-31 đi vào không phận từ một điểm trên mặt trụ và đi ra tại một điểm trên đáy trên của khối trụ. Đáy trên của khối trụ nằm trong mặt phẳng có phương trình là \(z = 43\) hay \(t = 0,5.\)
Suy ra, sau \(0,5\) giờ MiG-31 nằm ở vị trí \(\left\{ \begin{array}{l}x = 31 + 302 \cdot 0,5 = 182\\y = 10 + 840 \cdot 0,5 = 430\\z = 43\end{array} \right. \Rightarrow M\left( {182\,;430\,;43} \right)\).
Su-30 nằm ở vị trí \(\left\{ \begin{array}{l}x = 492 \cdot 0,5 = 246\\y = 35 + 720 \cdot 0,5 = 395\\z = 42\end{array} \right. \Rightarrow N\left( {246\,;395\,;42} \right)\).
Khoảng cách giữa hai máy bay cần tìm là
\(MN = \sqrt {{{\left( {246 - 182} \right)}^2} + {{\left( {395 - 430} \right)}^2} + {{\left( {42 - 43} \right)}^2}} \approx 72,95 \approx 73,0\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
30 Đề thi thử thpt quốc gia môn Toán có lời giải chi tiết mới nhất (Đề số 1)
-
CÂU TRẮC NGHIỆM ĐÚNG SAI
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 2)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 19)
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 2)
-
45 bài tập Xác suất có lời giải