Câu hỏi:
23/05/2025 40
Trong năm tới, một cửa hàng điện lạnh dự định kinh doanh hai loại máy điều hòa: điều hòa hai chiều và điều hòa một chiều với số vốn ban đầu không vượt quá \(1,2\) tỉ đồng.
Biết rằng, giá mua vào và lợi nhuận dự kiến được cho bởi bảng sau:
Điều hòa hai chiều
Điều hòa một chiều
Giá mua vào
20 triệu đồng/1 máy
10 triệu đồng/1 máy
Lợi nhuận dự kiến
3,5 triệu đồng/1 máy
2 triệu đồng/1 máy
Cửa hàng ước tính rằng nhu cầu của thị trường sẽ không vượt quá 100 máy cả hai loại. Cửa hàng cần đầu tư kinh doanh \(x\) loại máy hai chiều và \(y\) loại máy một chiều thì lợi nhuận thu được là lớn nhất. Tổng \({x^2} + {y^2}\) bằng bao nhiêu?
Trong năm tới, một cửa hàng điện lạnh dự định kinh doanh hai loại máy điều hòa: điều hòa hai chiều và điều hòa một chiều với số vốn ban đầu không vượt quá \(1,2\) tỉ đồng.
Biết rằng, giá mua vào và lợi nhuận dự kiến được cho bởi bảng sau:
|
|
Điều hòa hai chiều |
Điều hòa một chiều |
|
Giá mua vào |
20 triệu đồng/1 máy |
10 triệu đồng/1 máy |
|
Lợi nhuận dự kiến |
3,5 triệu đồng/1 máy |
2 triệu đồng/1 máy |
Cửa hàng ước tính rằng nhu cầu của thị trường sẽ không vượt quá 100 máy cả hai loại. Cửa hàng cần đầu tư kinh doanh \(x\) loại máy hai chiều và \(y\) loại máy một chiều thì lợi nhuận thu được là lớn nhất. Tổng \({x^2} + {y^2}\) bằng bao nhiêu?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án: 6800.
Giả sử cửa hàng dự định kinh doanh \(x\) máy điều hòa hai chiều và \(y\) máy điều hòa một chiều (điều kiện: \(x,y \in \mathbb{N}\)).
Khi đó, số vốn bỏ ra là \(20x + 10y\) (triệu đồng) và lợi nhuận thu được \(T = 3,5x + 2y\) (triệu đồng).
Theo giả thiết, \(x\) và \(y\) thỏa mãn các điều kiện: \(x \ge 0,\,y \ge 0,\,x + y \le 100,\,20x + 10y \le 1200\).
Bài toán đưa về: Tìm \(\left( {x\,;\,y} \right)\) là nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 100\\2x + y \le 120\end{array} \right.\,\,\,\left( I \right)\) sao cho \(T = 3,5x + 2y\) có giá trị lớn nhất.
Miền nghiệm của hệ bất phương trình \(\left( I \right)\) là miền tứ giác \(OABC\) với \(O\left( {0;\,0} \right)\), \(A\left( {0;\,100} \right)\), \(B\left( {20;\,80} \right)\), \(C\left( {60;\,0} \right)\).
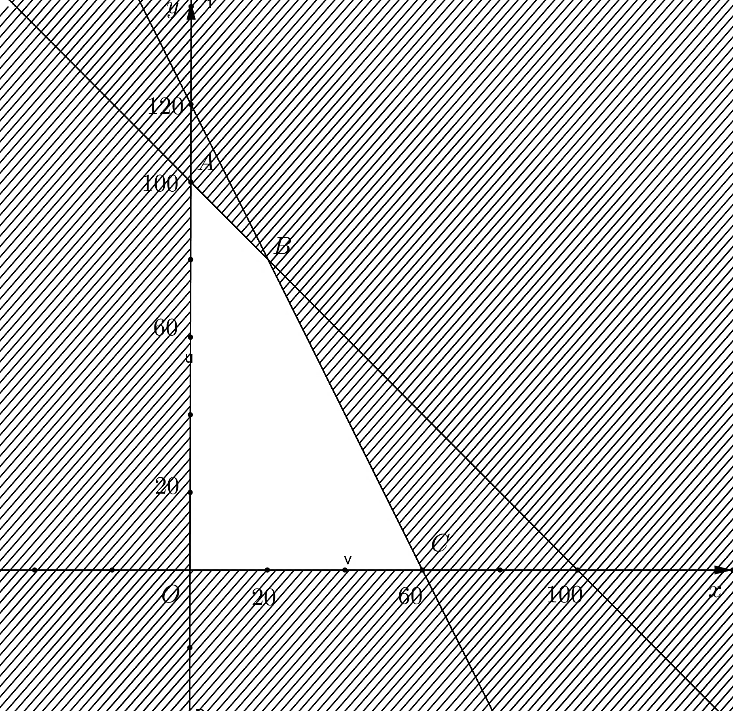
Thay tọa độ các đỉnh của tứ giác \(OABC\) vào biểu thức \(T = 3,5x + 2y\) ta được giá trị lớn nhất bằng 230 khi \(x = 20,\,y = 80\).
Vậy để thu được lợi nhuận lớn nhất cần đầu tư kinh doanh 20 máy điều hòa hai chiều và 80 máy điều hòa một chiều. Khi đó, ta có \({x^2} + {y^2} = {20^2} + {80^2} = 6800\).
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: 8.
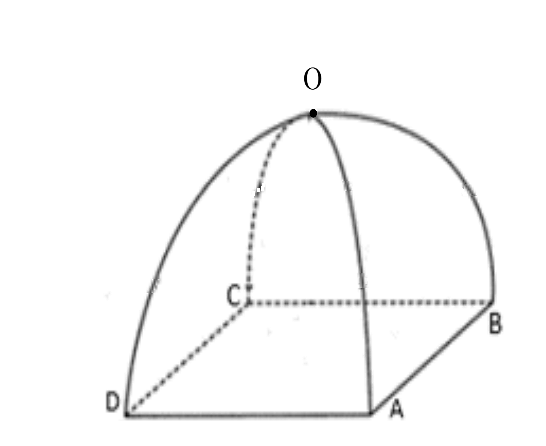
Ta có \(AB = 2\sqrt 2 \Rightarrow AC = 4.\) Chọn hệ trục \(Oxy\) như hình vẽ.
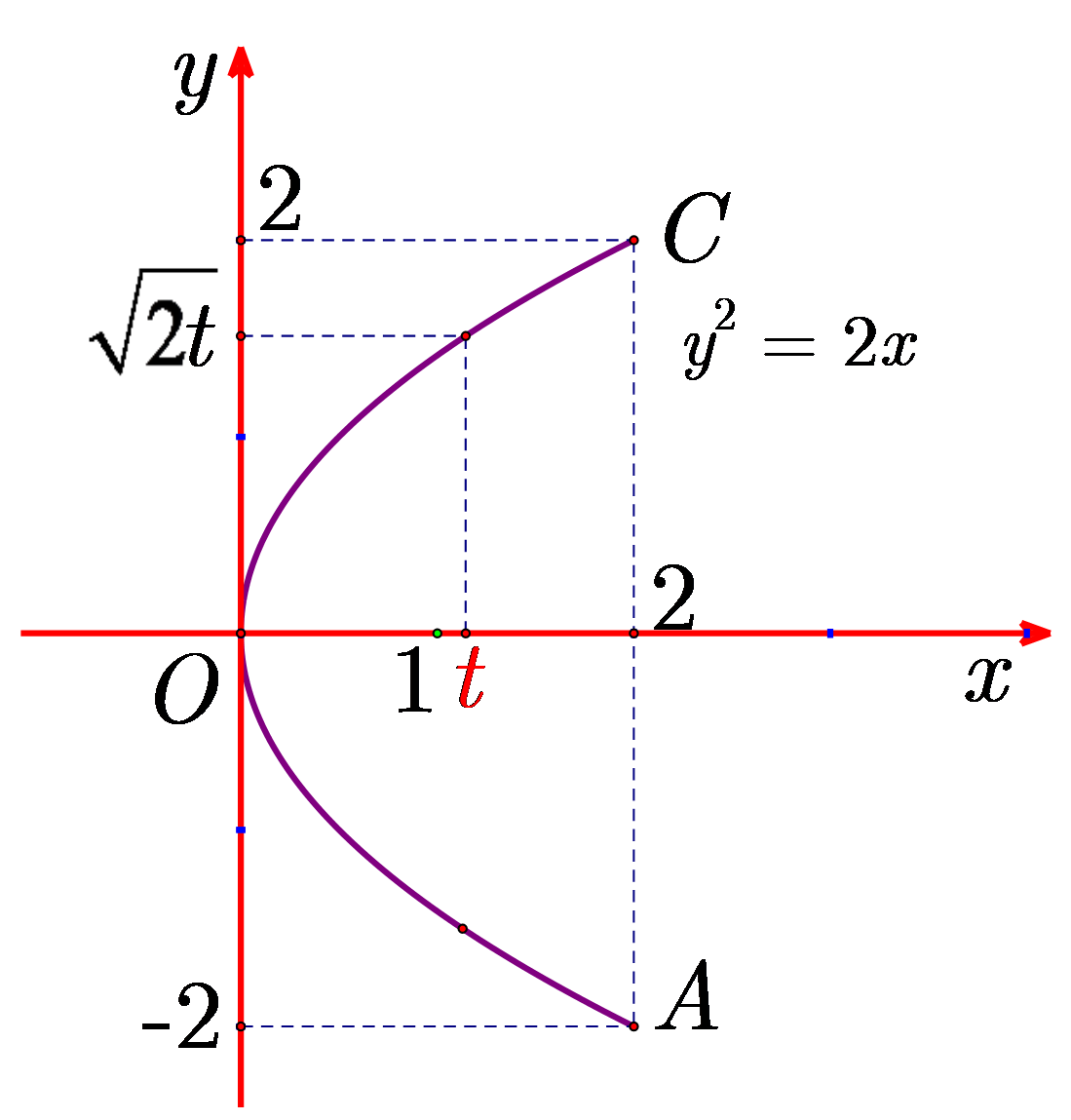
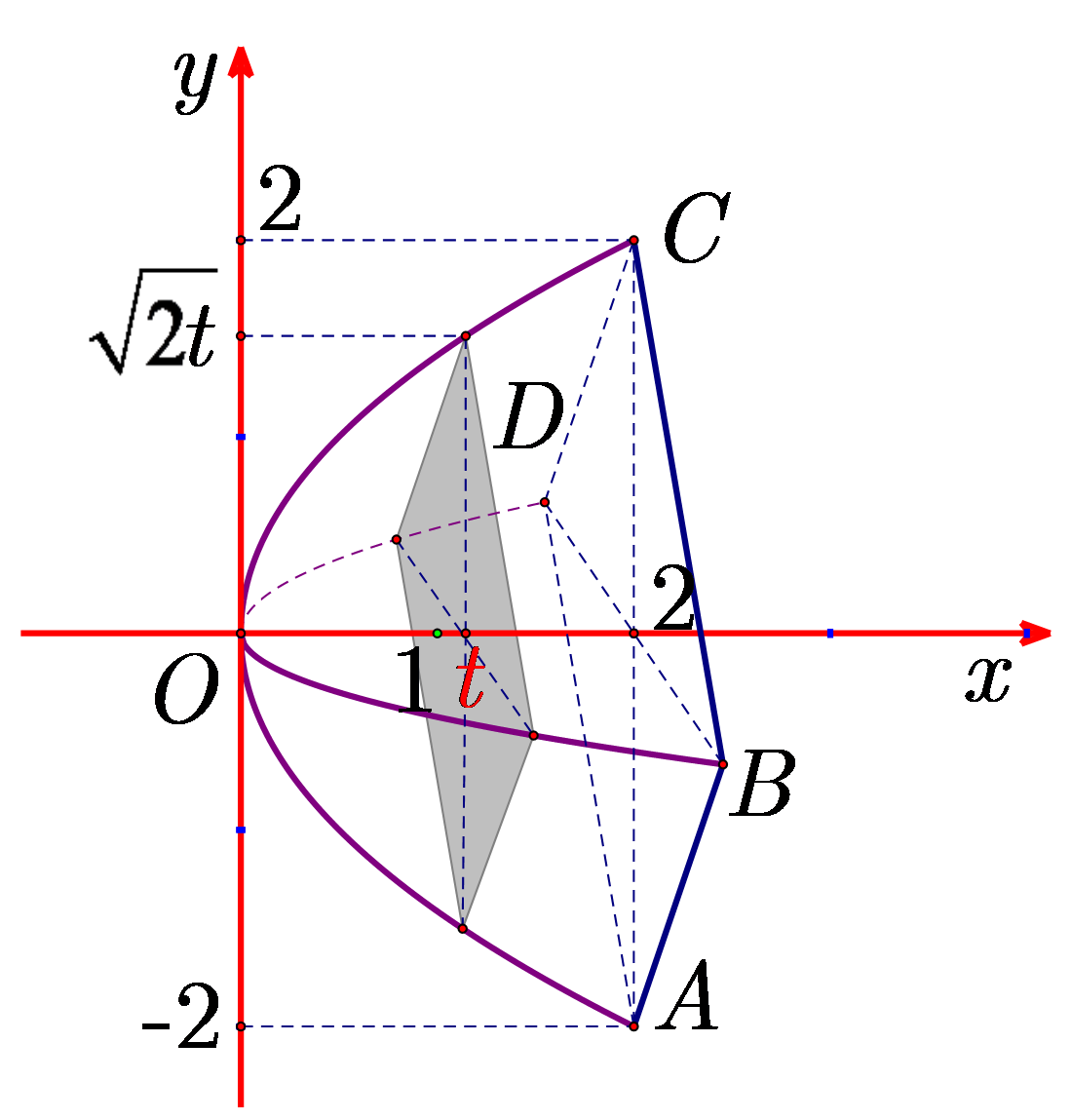
Khi đó, mặt cắt tại \(x = t\) là hình vuông có diện tích \(S\left( t \right) = \frac{1}{2}{\left( {2\sqrt {2t} } \right)^2} = 4t\).
Vậy thể tích của lều là \(V = \int\limits_0^2 {S\left( t \right){\rm{d}}t} = \int\limits_0^2 {4t{\rm{d}}t} = \left. {2{t^2}} \right|_0^2 = 8{\rm{ }}\left( {{{\rm{m}}^3}} \right).\)
Lời giải
Đáp án: 73,0.
Xác định các vectơ vận tốc:
Gọi \(\vec a:\) vectơ vận tốc của máy bay Su-30
\(\vec b:\) vectơ vận tốc của máy bay MiG-31
\(\vec c:\) vectơ vận tốc của gió
\({\vec u_1}:\) vectơ chỉ phương của đường thẳng quỹ đạo bay của máy bay Su-30
\({d_1}:\) đường thẳng quỹ đạo bay của máy bay Su-30
\({\vec u_2}:\) vectơ chỉ phương của đường thẳng quỹ đạo bay của máy bay MiG-31
\({d_2}:\) đường thẳng quỹ đạo bay của máy bay MiG-31
\(\left( T \right):\) mặt trụ có tâm \(C\left( {178\,;430\,;0} \right)\) bán kính \(r = 7.\)
\[\begin{array}{l}\left| {{{\vec v}_1}} \right| = \sqrt {{3^2} + {4^2} + {0^2}} = 5 \Rightarrow \vec a = \frac{{900}}{5}{{\vec v}_1} = \left( {540\,;720\,;0} \right)\\\left| {{{\vec v}_2}} \right| = 13 \Rightarrow \vec b = \frac{{910}}{{13}}{{\vec v}_2} = \left( {350\,;840\,;0} \right)\\\left| {\vec u} \right| = 5 \Rightarrow \vec c = \frac{{80}}{5}\vec u = \left( { - 48\,;0\,;64} \right)\\{{\vec u}_1} = \vec a + \vec c = \left( {492\,;720\,;64} \right) \Rightarrow {d_1}:\left\{ \begin{array}{l}x = 492t\\y = 35 + 720t\\z = 10 + 64t\end{array} \right.\\{{\vec u}_2} = \vec b + \vec c = \left( {302\,;840\,;64} \right) \Rightarrow {d_2}:\left\{ \begin{array}{l}x = 31 + 302t\\y = 10 + 840t\\z = 11 + 64t\end{array} \right.\\\left( T \right):{\left( {x - 178} \right)^2} + {\left( {y - 430} \right)^2} = {7^2}.\end{array}\]
Vì không phận cấm bay có độ cao \(43{\rm{ km}}\) nên MiG-31 vào trong không phận thì độ cao tối đa của máy bay là \(z \le 43 \Rightarrow 11 + 64t \le 43 \Leftrightarrow t \le 0,5.\)
Tìm giao điểm của \({d_2}\) và \(\left( T \right)\).
Xét phương trình: \({\left( {31 + 302t - 178} \right)^2} + {\left( {10 + 840t - 430} \right)^2} = 49\)
\( \Leftrightarrow 796804{t^2} - 794388t + 197960 = 0 \Leftrightarrow \left[ \begin{array}{l}t = 0,51 > 5\\t = 0,49 < 5\end{array} \right.\).
Dễ dàng nhận thấy MiG-31 đi vào không phận từ một điểm trên mặt trụ và đi ra tại một điểm trên đáy trên của khối trụ. Đáy trên của khối trụ nằm trong mặt phẳng có phương trình là \(z = 43\) hay \(t = 0,5.\)
Suy ra, sau \(0,5\) giờ MiG-31 nằm ở vị trí \(\left\{ \begin{array}{l}x = 31 + 302 \cdot 0,5 = 182\\y = 10 + 840 \cdot 0,5 = 430\\z = 43\end{array} \right. \Rightarrow M\left( {182\,;430\,;43} \right)\).
Su-30 nằm ở vị trí \(\left\{ \begin{array}{l}x = 492 \cdot 0,5 = 246\\y = 35 + 720 \cdot 0,5 = 395\\z = 42\end{array} \right. \Rightarrow N\left( {246\,;395\,;42} \right)\).
Khoảng cách giữa hai máy bay cần tìm là
\(MN = \sqrt {{{\left( {246 - 182} \right)}^2} + {{\left( {395 - 430} \right)}^2} + {{\left( {42 - 43} \right)}^2}} \approx 72,95 \approx 73,0\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
30 Đề thi thử thpt quốc gia môn Toán có lời giải chi tiết mới nhất (Đề số 1)
-
CÂU TRẮC NGHIỆM ĐÚNG SAI
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 2)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 19)
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 2)
-
45 bài tập Xác suất có lời giải