Câu hỏi:

26/05/2025 15

Các điểm biểu diễn hai nghiệm x₁, x₂ của phương trình x² – 2x – 1 = 0 trên trục Ox của mặt phẳng tọa độ Oxy cùng với điểm C(1; 5) tạo thành một tam giác có diện tích là

A. \(2\sqrt 5 .\)

B. \(3\sqrt 5 .\)

C. \(3\sqrt 2 .\)

D. \(5\sqrt 2 .\)

Câu hỏi trong đề: 10 bài tập Tính tổng, tích và giá trị của biểu thức đối xứng giữa các nghiệm x1, x2 của phương trình bậc hai một ẩn mà không giải phương trình có lời giải !!

Bắt đầu thi

Trả lời:

Giải bởi Vietjack

Đáp án đúng là: D

Phương trình x² – 2x – 1 = 0 có ∆' = (–1)² – 1.(–1) = 2 > 0 nên phương trình có hai nghiệm phân biệt.

Theo định lí Viète, ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\\{x_1}{x_2} = - 1\end{array} \right..\)

Gọi A và B lần lượt là điểm biểu diễn x₁ và x₂ trên Ox.

Ta có x₁x₂ = –1 < 0 nên hai nghiệm x₁

, x₂ trái dấu nhau, do đó hai điểm A(x₁; 0) và B(x₂; 0) biểu diễn hai nghiệm x₁, x₂ nằm trên trục Ox và nằm về hai phía của trục Oy.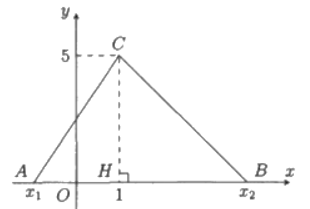

Ta có AB = |x₁ – x₂|.

Suy ra AB² = |x₁ – x₂|² = (x₁ + x₂)² – 4x₁x₂ = 2² – 4.(–1) = 8.

Do đó \(AB = \sqrt 8 = 2\sqrt 2 .\)

Gọi H là hình chiếu của điểm C(1; 5) trên Ox, khi đó CH = |y_C| = 5.

Vậy diện tích tam giác ABC là:

\({S_{\Delta ABC}} = \frac{1}{2}CH \cdot AB = \frac{1}{2} \cdot 5 \cdot 2\sqrt 2 = 5\sqrt 2 \) (đơn vị diện tích).

Bình luận

Câu 1:

Gọi x₁, x₂ là hai nghiệm của phương trình –x² – 5x – 3 = 0, khi đó ta có

A. x₁ + x₂ = –5, x₁x₂ = 3.

B. x₁ + x₂ = –5, x₁x₂ = –3.

C. x₁ + x₂ = 5, x₁x₂ = –3.

D. x₁ + x₂ = 3, x₁x₂ = –5.

Xem đáp án » 26/05/2025 45

Câu 2:

Nếu phương trình ax² + bx + c = 0 (a ≠ 0) có hai nghiệm x₁, x₂ thì

A. \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = \frac{b}{a}}\\{{x_1}{x_2} = \frac{c}{a}}\end{array}} \right..\)

B. \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = - \frac{b}{a}}\\{{x_1}{x_2} = \frac{c}{a}}\end{array}} \right..\)

C. \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = - \frac{b}{a}}\\{{x_1}{x_2} = \frac{a}{c}}\end{array}} \right..\)

D. \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = - \frac{b}{a}}\\{{x_1}{x_2} = - \frac{c}{a}}\end{array}} \right..\)

Xem đáp án » 26/05/2025 31

Câu 3:

Cho phương trình x² – 7x + 11 = 0 có hai nghiệm và gọi S và P lần lượt là tổng và tích hai nghiệm đó. Khi đó S + P bằng

A. 4.

B. 7.

C. 11.

D. 18.

Xem đáp án » 26/05/2025 24

Câu 4:

Cho phương trình x² + 200x – 1 = 0 có hai nghiệm phân biệt x₁, x₂. Giá trị của biểu thức \(C = \frac{{100\left| {{x_1} - {x_2}} \right|}}{{x_1^2{x_2} + {x_1}x_2^2}}\) là

A. \(2\sqrt {10001} .\)

B. \(\frac{{\sqrt {10001} }}{2}.\)

C. \(\frac{{\sqrt {10001} }}{{100}}.\)

D. \(\sqrt {10001} .\)

Xem đáp án » 26/05/2025 17

Câu 5:

Khoảng cách giữa hai điểm biểu diễn hai nghiệm của phương trình x² – x – 2 = 0 trên trục số bằng bao nhiêu?

A. \(\sqrt 3 .\)

B. 3.

C. \(\sqrt 5 .\)

D. 5.

Xem đáp án » 26/05/2025 16

Câu 6:

Cho phương trình 9x² – 100x + 25 = 0 có hai nghiệm dương x₁, x₂. Giá trị của biểu thức \(B = \frac{{x_1^2 + x_2^2}}{{\sqrt {{x_1}} + \sqrt {{x_2}} }}\) là

A. \(\frac{{995}}{{11}}.\)

B. \[\frac{{955\sqrt {130} }}{{351}}\]

C. \(\frac{{235\sqrt {85} }}{{459}}.\)

D. \(\frac{{955}}{{117}}.\)

Xem đáp án » 26/05/2025 15

Các điểm biểu diễn hai nghiệm x₁, x₂ của phương trình x² – 2x – 1 = 0 trên trục Ox của mặt phẳng tọa độ Oxy cùng với điểm C(1; 5) tạo thành một tam giác có diện tích là

Cấp tốc 789+ thi vào lớp 10 môn Toán

Cấp tốc 789+ thi vào lớp 10 môn Ngữ Văn

Cấp tốc 789+ thi vào lớp 10 môn Tiếng Anh

Lớp 9 - Siêu trọng tâm Toán, Văn, Anh

Bình luận

Gọi x₁, x₂ là hai nghiệm của phương trình –x² – 5x – 3 = 0, khi đó ta có

Nếu phương trình ax² + bx + c = 0 (a ≠ 0) có hai nghiệm x₁, x₂ thì

Cho phương trình x² – 7x + 11 = 0 có hai nghiệm và gọi S và P lần lượt là tổng và tích hai nghiệm đó. Khi đó S + P bằng

Cho phương trình x² + 200x – 1 = 0 có hai nghiệm phân biệt x₁, x₂. Giá trị của biểu thức \(C = \frac{{100\left| {{x_1} - {x_2}} \right|}}{{x_1^2{x_2} + {x_1}x_2^2}}\) là

Khoảng cách giữa hai điểm biểu diễn hai nghiệm của phương trình x² – x – 2 = 0 trên trục số bằng bao nhiêu?

Cho phương trình 9x² – 100x + 25 = 0 có hai nghiệm dương x₁, x₂. Giá trị của biểu thức \(B = \frac{{x_1^2 + x_2^2}}{{\sqrt {{x_1}} + \sqrt {{x_2}} }}\) là

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

Các điểm biểu diễn hai nghiệm x1, x2 của phương trình x2 – 2x – 1 = 0 trên trục Ox của mặt phẳng tọa độ Oxy cùng với điểm C(1; 5) tạo thành một tam giác có diện tích là

Bình luận

Gọi x1, x2 là hai nghiệm của phương trình –x2 – 5x – 3 = 0, khi đó ta có

Nếu phương trình ax2 + bx + c = 0 (a ≠ 0) có hai nghiệm x1, x2 thì

Cho phương trình x2 – 7x + 11 = 0 có hai nghiệm và gọi S và P lần lượt là tổng và tích hai nghiệm đó. Khi đó S + P bằng

Cho phương trình x2 + 200x – 1 = 0 có hai nghiệm phân biệt x1, x2. Giá trị của biểu thức \(C = \frac{{100\left| {{x_1} - {x_2}} \right|}}{{x_1^2{x_2} + {x_1}x_2^2}}\) là

Khoảng cách giữa hai điểm biểu diễn hai nghiệm của phương trình x2 – x – 2 = 0 trên trục số bằng bao nhiêu?

Cho phương trình 9x2 – 100x + 25 = 0 có hai nghiệm dương x1, x2. Giá trị của biểu thức \(B = \frac{{x_1^2 + x_2^2}}{{\sqrt {{x_1}} + \sqrt {{x_2}} }}\) là

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Các điểm biểu diễn hai nghiệm x₁, x₂ của phương trình x² – 2x – 1 = 0 trên trục Ox của mặt phẳng tọa độ Oxy cùng với điểm C(1; 5) tạo thành một tam giác có diện tích là

Gọi x₁, x₂ là hai nghiệm của phương trình –x² – 5x – 3 = 0, khi đó ta có

Nếu phương trình ax² + bx + c = 0 (a ≠ 0) có hai nghiệm x₁, x₂ thì

Cho phương trình x² – 7x + 11 = 0 có hai nghiệm và gọi S và P lần lượt là tổng và tích hai nghiệm đó. Khi đó S + P bằng

Cho phương trình x² + 200x – 1 = 0 có hai nghiệm phân biệt x₁, x₂. Giá trị của biểu thức \(C = \frac{{100\left| {{x_1} - {x_2}} \right|}}{{x_1^2{x_2} + {x_1}x_2^2}}\) là

Khoảng cách giữa hai điểm biểu diễn hai nghiệm của phương trình x² – x – 2 = 0 trên trục số bằng bao nhiêu?

Cho phương trình 9x² – 100x + 25 = 0 có hai nghiệm dương x₁, x₂. Giá trị của biểu thức \(B = \frac{{x_1^2 + x_2^2}}{{\sqrt {{x_1}} + \sqrt {{x_2}} }}\) là