Cho đường tròn tâm O và hai đường kính AB, CD. Biết rằng \[\widehat {AOC} = 60^\circ \]. Chọn khẳng định sai trong các khẳng định dưới đây.
A. \[\widehat {BOC} = 120^\circ \].
B. \[\widehat {ABC} = 60^\circ \].
C. \[\widehat {ADC} = 30^\circ \].
D. \[\widehat {BAC} = \widehat {CDB} = 60^\circ \].
Câu hỏi trong đề: 10 bài tập Tính số đo của góc nội tiếp có lời giải !!
Quảng cáo
Trả lời:
Đáp án đúng là: B
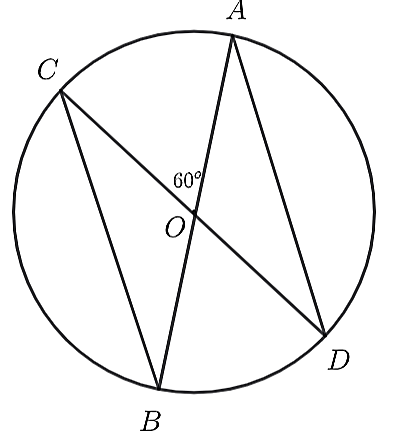
Ta có:
\[\widehat {AOC} + \widehat {BOC} = 180^\circ \] (kề bù)
Do đó, \[\widehat {BOC} = 180^\circ - 60^\circ = 120^\circ \].
Suy ra A đúng.
Lại có \[\widehat {ABC}\] và \[\widehat {ADC}\] là các góc nội tiếp chắn cung AC, \[\widehat {AOC}\] là góc ở tâm chắn cung AC.
Do đó, \[\widehat {ABC} = \widehat {ADC} = \frac{1}{2}\widehat {AOC} = \frac{1}{2}.60^\circ = 30^\circ \].
Do đó, B sai và C đúng.
Có \[\widehat {BAC} = \widehat {BDC} = \frac{1}{2}\widehat {BOC} = \frac{1}{2}.120^\circ = 60^\circ \].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. 45°.
B. 60°.
C. 90°.
D. 30°.
Lời giải
Đáp án đúng là: C
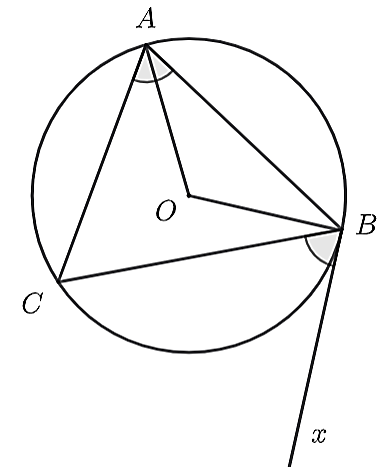
Ta có
\[\widehat {xBO} = \widehat {xBC} + \widehat {CBO}\]
\[\widehat {xBO} = \widehat A + \frac{{180^\circ - \widehat {COB}}}{2}\] (do ∆OBC cân tại O)
\[\widehat {xBO} = \widehat A + 90^\circ - \widehat A\] = 90°.
(\[\widehat A = \frac{{\widehat {COB}}}{2}\] vì góc nội tiếp và góc ở tâm cùng chắn cung CB)
Câu 2
A. \[\widehat {IAC} = \widehat {CDB} = 70^\circ \].
B. \[\widehat {IAC} = \widehat {CDB} = 60^\circ \].
C. \[\widehat {IAC} = 60^\circ ,\widehat {CDB} = 70^\circ .\]
D. \[\widehat {IAC} = 70^\circ ,\widehat {CDB} = 60^\circ \].
Lời giải
Đáp án đúng là: B
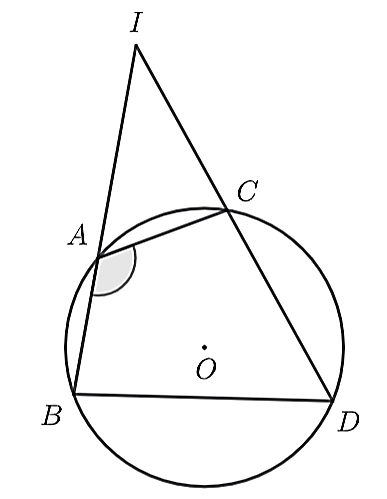
Ta có:
\[\widehat {CAB} = 120^\circ \]
nên \[\widehat {CAI} = 180^\circ - \widehat {CAB} = 180^\circ - 120^\circ = 60^\circ \].
Ta có: sdlớn = 2\[\widehat {CAB} = 240^\circ \].
Do đó, sđnhỏ = 360° − 240° = 120°.
Suy ra (góc nội tiếp).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. 45°.
B. 60°.
C. 90°.
D. 30°.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.