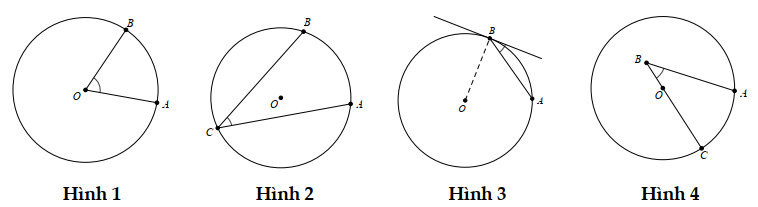
Sử dụng dữ kiện bài toán dưới đây để trả lời Câu 6, 7.
Cho tam giác ABC có ba góc nhọn, đường cao AH và nội tiếp đường tròn (O), đường kính AM.
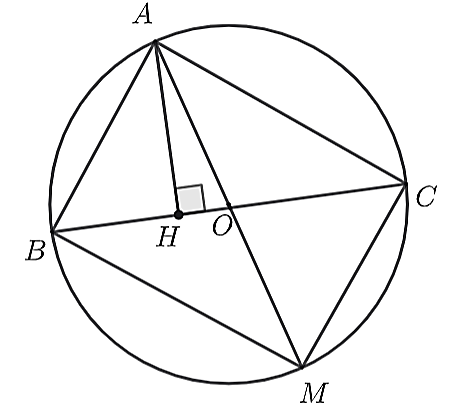
Sử dụng dữ kiện bài toán dưới đây để trả lời Câu 6, 7.
Cho tam giác ABC có ba góc nhọn, đường cao AH và nội tiếp đường tròn (O), đường kính AM.

Số đo góc ACM là
A. 100°.
B. 90°.
C. 110°.
D. 100°.
Câu hỏi trong đề: 10 bài tập Tính số đo của góc nội tiếp có lời giải !!
Quảng cáo
Trả lời:
Đáp án đúng là: B
Ta có \[\widehat {ACM} = 90^\circ \] (góc nội tiếp chắn nửa đường tròn)
Câu hỏi cùng đoạn
Câu 2:
Số đo góc ABM là
A. 90°.
B. 80°.
C. 110°.
D. 120°.
Đáp án đúng là: A
Ta có \[\widehat {ABM} = 90^\circ \] (góc nội tiếp chắn nửa đường tròn)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. 45°.
B. 60°.
C. 90°.
D. 30°.
Lời giải
Đáp án đúng là: C
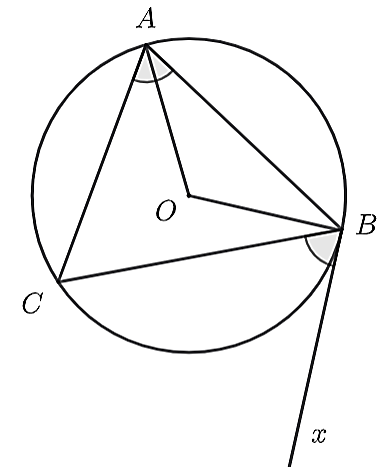
Ta có
\[\widehat {xBO} = \widehat {xBC} + \widehat {CBO}\]
\[\widehat {xBO} = \widehat A + \frac{{180^\circ - \widehat {COB}}}{2}\] (do ∆OBC cân tại O)
\[\widehat {xBO} = \widehat A + 90^\circ - \widehat A\] = 90°.
(\[\widehat A = \frac{{\widehat {COB}}}{2}\] vì góc nội tiếp và góc ở tâm cùng chắn cung CB)
Câu 2
A. \[\widehat {IAC} = \widehat {CDB} = 70^\circ \].
B. \[\widehat {IAC} = \widehat {CDB} = 60^\circ \].
C. \[\widehat {IAC} = 60^\circ ,\widehat {CDB} = 70^\circ .\]
D. \[\widehat {IAC} = 70^\circ ,\widehat {CDB} = 60^\circ \].
Lời giải
Đáp án đúng là: B
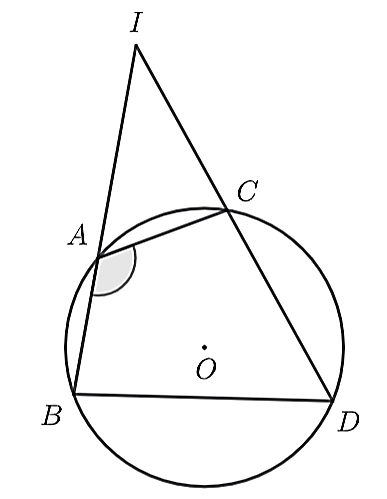
Ta có:
\[\widehat {CAB} = 120^\circ \]
nên \[\widehat {CAI} = 180^\circ - \widehat {CAB} = 180^\circ - 120^\circ = 60^\circ \].
Ta có: sdlớn = 2\[\widehat {CAB} = 240^\circ \].
Do đó, sđnhỏ = 360° − 240° = 120°.
Suy ra (góc nội tiếp).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. 45°.
B. 60°.
C. 90°.
D. 30°.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.