Để hạn chế vi phạm thời gian làm việc đối với công nhân, giám đốc công ty quyết định xử lý bằng cách phạt tiền. Nhờ sự giám sát chặt chẽ của các quản đốc, giám đốc công ty biết được trong một tháng, giữa tỉ lệ công nhân vi phạm đúng \(k\) lần \(\left( {1 \le k \le 2} \right)\) là \({t_k} = \frac{{{N_k}}}{N}\) (trong đó \({N_k}\) là số công nhân vi phạm đúng \(k\) lần, \(N\) là tổng số công nhân) và mức phạt mỗi lần vi phạm có mối liên hệ như sau:
Nếu mỗi công nhân nộp phạt \(x\) nghìn đồng \(\left( {60 \le x \le 300} \right)\) khi vi phạm lần thứ nhất và nộp phạt \(x - 20\) nghìn đồng khi vi phạm lần thứ hai thì \({t_1} = \frac{{36}}{{x + 10}}\) và \({t_2} = \frac{4}{{x - 30}}\) (không có công nhân nào vi phạm quá hai lần).
Biết rằng \(N\) không đổi và bằng \(2\,400\). Tổng số tiền nộp phạt của các công nhân vi phạm trong một tháng ít nhất là bao nhiêu triệu đồng? (làm tròn kết quả đến hàng đơn vị).
Để hạn chế vi phạm thời gian làm việc đối với công nhân, giám đốc công ty quyết định xử lý bằng cách phạt tiền. Nhờ sự giám sát chặt chẽ của các quản đốc, giám đốc công ty biết được trong một tháng, giữa tỉ lệ công nhân vi phạm đúng \(k\) lần \(\left( {1 \le k \le 2} \right)\) là \({t_k} = \frac{{{N_k}}}{N}\) (trong đó \({N_k}\) là số công nhân vi phạm đúng \(k\) lần, \(N\) là tổng số công nhân) và mức phạt mỗi lần vi phạm có mối liên hệ như sau:
Nếu mỗi công nhân nộp phạt \(x\) nghìn đồng \(\left( {60 \le x \le 300} \right)\) khi vi phạm lần thứ nhất và nộp phạt \(x - 20\) nghìn đồng khi vi phạm lần thứ hai thì \({t_1} = \frac{{36}}{{x + 10}}\) và \({t_2} = \frac{4}{{x - 30}}\) (không có công nhân nào vi phạm quá hai lần).
Biết rằng \(N\) không đổi và bằng \(2\,400\). Tổng số tiền nộp phạt của các công nhân vi phạm trong một tháng ít nhất là bao nhiêu triệu đồng? (làm tròn kết quả đến hàng đơn vị).
Quảng cáo
Trả lời:
Ta có: \({t_k} = \frac{{{N_k}}}{N} \Leftrightarrow {N_k} = N \cdot {t_k}\).
Số công nhân vi phạm đúng một lần là \({N_1} = N \cdot {t_1} = \frac{{36N}}{{x + 10}}\).
Suy ra số tiền nộp phạt từ \({N_1}\) công nhân này là: \({N_1} \cdot x = \frac{{36Nx}}{{x + 10}}\) (nghìn đồng).
Số công nhân vi phạm đúng hai lần là \({N_2} = N \cdot {t_2} = \frac{{4N}}{{x - 30}}\).
Suy ra số tiền nộp phạt từ \({N_2}\) công nhân này là: \({N_2} \cdot \left( {x + x - 20} \right) = \frac{{4N\left( {2x - 20} \right)}}{{x - 30}}\) (nghìn đồng).
Vậy tổng số tiền nộp phạt của các công nhân vi phạm trong một tháng là:
\(f\left( x \right) = \frac{{36Nx}}{{x + 10}} + \frac{{4N\left( {2x - 20} \right)}}{{x - 30}}\)\( = 4N\left( {\frac{{9x}}{{x + 10}} + \frac{{2x - 20}}{{x - 30}}} \right)\) (nghìn đồng).
Xét hàm số \(f\left( x \right)\) với \(x \in \left[ {60;300} \right]\), ta có: \(f'\left( x \right) = 4N \cdot \left[ {\frac{{90}}{{{{\left( {x + 10} \right)}^2}}} - \frac{{40}}{{{{\left( {x - 30} \right)}^2}}}} \right]\).
Cho \(f'\left( x \right) = 0 \Leftrightarrow \frac{{90}}{{{{\left( {x + 10} \right)}^2}}} - \frac{{40}}{{{{\left( {x - 30} \right)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 110\quad (TM)\\x = 14\quad \;\,(L)\end{array} \right.\).
Ta có bảng biến thiên:

Từ bảng biến thiên ta thấy tổng số tiền nộp phạt của các công nhân vi phạm trong một tháng ít nhất là: \(43N = 43 \cdot 2\,400 = 103\,200\) (nghìn đồng) \( \approx 103\) (triệu đồng).
Đáp án: \(103\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
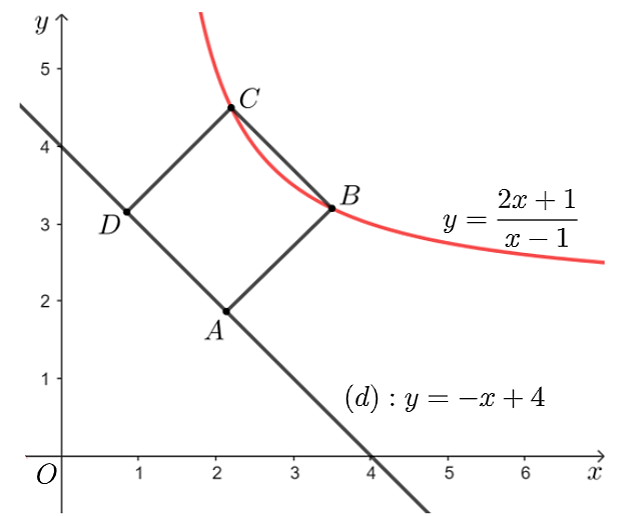
Gọi \(\left( {{d_1}} \right):y = - x + m\) (với \(m > 4\)) song song với \(\left( d \right):y = - x + 4\) và cắt \(\left( C \right):y = \frac{{2x + 1}}{{x - 1}}\) tại hai điểm phân biệt \(B,C\)\(\left( {{x_B}\,;\,{x_C} > 1} \right)\).
Phương trình hoành độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( C \right)\): \(\frac{{2x + 1}}{{x - 1}} = - x + m \Leftrightarrow {x^2} + \left( {1 - m} \right)x + m + 1 = 0.\)
\(\Delta = {m^2} - 6m - 3 > 0 \Leftrightarrow \left[ \begin{array}{l}m > 3 + 2\sqrt 3 \\m < 3 - 2\sqrt 3 \end{array} \right. \Leftrightarrow m > 3 + 2\sqrt 3 \) (vì \(m > 4\)) (1).
Khi đó ta có: \(\left\{ \begin{array}{l}{x_C} + {x_B} = m - 1\\{x_C} \cdot {x_B} = m + 1\end{array} \right.\).
Suy ra \(CB = \sqrt {{{\left( {{x_B} - {x_C}} \right)}^2} + {{\left( {{y_B} - {y_C}} \right)}^2}} = \sqrt {{{\left( {{x_B} - {x_C}} \right)}^2} + {{\left( { - {x_B} + m + {x_C} - m} \right)}^2}} = \sqrt {2{{\left( {{x_B} - {x_C}} \right)}^2}} \).
\( \Rightarrow C{B^2} = 2{\left( {{x_B} - {x_C}} \right)^2} = 2{\left( {{x_B} + {x_C}} \right)^2} - 8{x_B} \cdot {x_C} = 2{m^2} - 12m - 6\).
Mặt khác chọn \(I\left( {0;4} \right) \in \left( d \right)\), ta có khoảng cách giữa hai đường thẳng \(\left( d \right);\left( {{d_1}} \right)\) là:
\(AB = d\left( {I,\left( {{d_1}} \right)} \right) = \frac{{\left| {4 - m} \right|}}{{\sqrt 2 }} = \frac{{m - 4}}{{\sqrt 2 }}\).
Để \(ABCD\) là hình vuông thì \(A{B^2} = B{C^2} \Leftrightarrow \frac{{{{\left( {m - 4} \right)}^2}}}{2} = 2{m^2} - 12m - 6 \Leftrightarrow m = \frac{{8 \pm 2\sqrt {37} }}{3}\).
Kết hợp điều kiện (1) suy ra \(m = \frac{{8 + 2\sqrt {37} }}{3}\).
Vậy khoảng cách giữa hai cột đèn bên bờ hồ bằng \(\frac{{\frac{{8 + 2\sqrt {37} }}{3} - 4}}{{\sqrt 2 }} \approx 1,92.\)
Đáp án: \(1,92\).
Câu 2
Lời giải
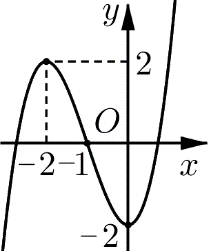
Ta có \(y = - x + 3 - \frac{1}{{x + 2}} \Rightarrow y' = - 1 + \frac{1}{{{{\left( {x + 2} \right)}^2}}} = \frac{{ - {x^2} - 4x - 3}}{{{{\left( {x + 2} \right)}^2}}}\).
Với \(y' = 0 \Leftrightarrow - {x^2} - 4x - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1 \notin \left[ { - 4; - 2} \right)\\x = - 3 \in \left[ { - 4; - 2} \right)\end{array} \right.\).
Ta có bảng biến thiên:
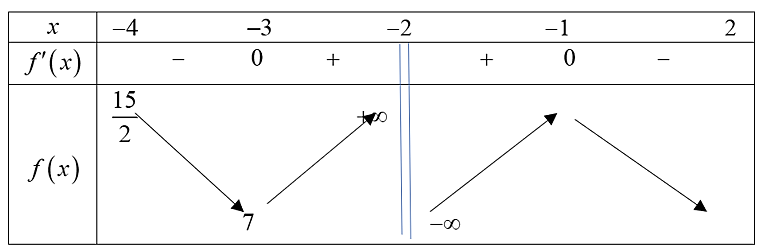
Dựa vào đồ thị \(\mathop {\min }\limits_{\left[ { - 4; - 2} \right)} y = 7\). Chọn C.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.