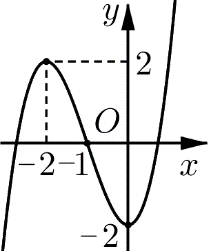
Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?

Quảng cáo
Trả lời:
Dựa vào đồ thị, ta thấy đồ thị hàm số là hàm bậc ba và\(\mathop {\lim }\limits_{x \to + \infty } y = + \infty \) nên \(a > 0\), suy ra loại A, C. Đồ thị hàm số đi qua điểm \(\left( { - 1;0} \right)\) nên chọn đáp án B. Chọn B.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
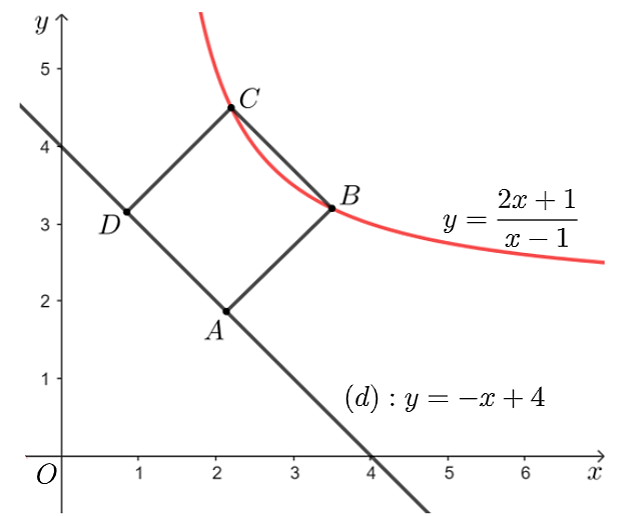
Gọi \(\left( {{d_1}} \right):y = - x + m\) (với \(m > 4\)) song song với \(\left( d \right):y = - x + 4\) và cắt \(\left( C \right):y = \frac{{2x + 1}}{{x - 1}}\) tại hai điểm phân biệt \(B,C\)\(\left( {{x_B}\,;\,{x_C} > 1} \right)\).
Phương trình hoành độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( C \right)\): \(\frac{{2x + 1}}{{x - 1}} = - x + m \Leftrightarrow {x^2} + \left( {1 - m} \right)x + m + 1 = 0.\)
\(\Delta = {m^2} - 6m - 3 > 0 \Leftrightarrow \left[ \begin{array}{l}m > 3 + 2\sqrt 3 \\m < 3 - 2\sqrt 3 \end{array} \right. \Leftrightarrow m > 3 + 2\sqrt 3 \) (vì \(m > 4\)) (1).
Khi đó ta có: \(\left\{ \begin{array}{l}{x_C} + {x_B} = m - 1\\{x_C} \cdot {x_B} = m + 1\end{array} \right.\).
Suy ra \(CB = \sqrt {{{\left( {{x_B} - {x_C}} \right)}^2} + {{\left( {{y_B} - {y_C}} \right)}^2}} = \sqrt {{{\left( {{x_B} - {x_C}} \right)}^2} + {{\left( { - {x_B} + m + {x_C} - m} \right)}^2}} = \sqrt {2{{\left( {{x_B} - {x_C}} \right)}^2}} \).
\( \Rightarrow C{B^2} = 2{\left( {{x_B} - {x_C}} \right)^2} = 2{\left( {{x_B} + {x_C}} \right)^2} - 8{x_B} \cdot {x_C} = 2{m^2} - 12m - 6\).
Mặt khác chọn \(I\left( {0;4} \right) \in \left( d \right)\), ta có khoảng cách giữa hai đường thẳng \(\left( d \right);\left( {{d_1}} \right)\) là:
\(AB = d\left( {I,\left( {{d_1}} \right)} \right) = \frac{{\left| {4 - m} \right|}}{{\sqrt 2 }} = \frac{{m - 4}}{{\sqrt 2 }}\).
Để \(ABCD\) là hình vuông thì \(A{B^2} = B{C^2} \Leftrightarrow \frac{{{{\left( {m - 4} \right)}^2}}}{2} = 2{m^2} - 12m - 6 \Leftrightarrow m = \frac{{8 \pm 2\sqrt {37} }}{3}\).
Kết hợp điều kiện (1) suy ra \(m = \frac{{8 + 2\sqrt {37} }}{3}\).
Vậy khoảng cách giữa hai cột đèn bên bờ hồ bằng \(\frac{{\frac{{8 + 2\sqrt {37} }}{3} - 4}}{{\sqrt 2 }} \approx 1,92.\)
Đáp án: \(1,92\).
Câu 2
Lời giải
Ta có \(y = - x + 3 - \frac{1}{{x + 2}} \Rightarrow y' = - 1 + \frac{1}{{{{\left( {x + 2} \right)}^2}}} = \frac{{ - {x^2} - 4x - 3}}{{{{\left( {x + 2} \right)}^2}}}\).
Với \(y' = 0 \Leftrightarrow - {x^2} - 4x - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1 \notin \left[ { - 4; - 2} \right)\\x = - 3 \in \left[ { - 4; - 2} \right)\end{array} \right.\).
Ta có bảng biến thiên:
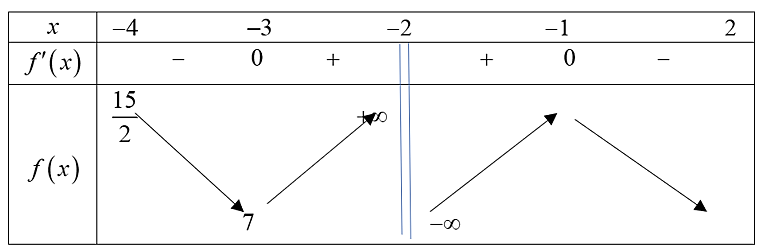
Dựa vào đồ thị \(\mathop {\min }\limits_{\left[ { - 4; - 2} \right)} y = 7\). Chọn C.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.