Ông An xây một bể bơi, ban đầu có dạng là hình hộp chữ nhật \(ABCD.A'B'C'D'\). Sau đó ông làm lại mặt đáy như hình vẽ.
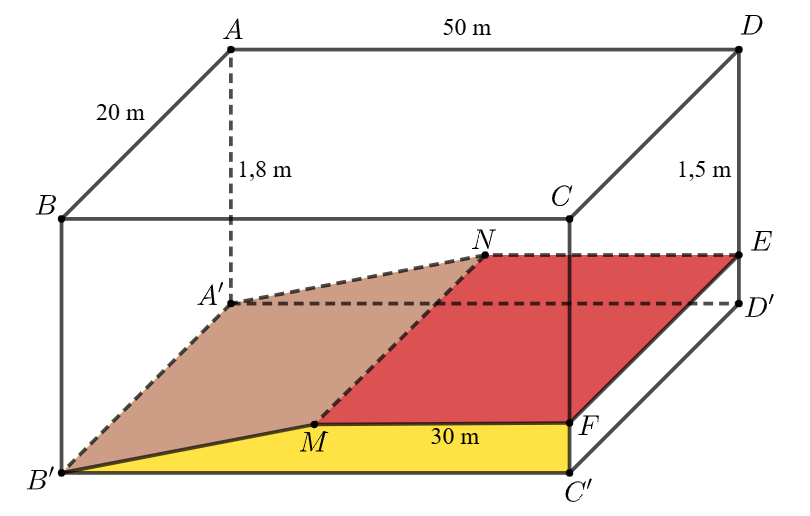
Biết rằng \(A'B'MN\) và \(MNEF\) là các hình chữ nhật, \(\left( {MNEF} \right){\rm{//}}\left( {A'B'C'D'} \right)\), \(AB = 20\,{\rm{m}}\), \(AD = 50\,{\rm{m}}\), \(AA' = 1,8\,{\rm{m}}\), \(MF = 30\,{\rm{m}}\), \(DE = 1,5\,{\rm{m}}\).
a) Cạnh BC của thành bể vuông góc với đường thẳng chứa MN của đáy bể.
b) Góc giữa thành bể \[ABB'A'\] và mặt phẳng chứa phần đáy \[\left( {MNA'B'} \right)\] gần bằng \(65^\circ 45'\).
c) Khoảng cách từ điểm B của góc bể đến mặt phẳng chứa phần đáy \[\left( {MNA'B'} \right)\] xấp xỉ bằng \(1,6599\,\,{\rm{m}}\).
d) Ông An bơm nước vào bể để phục vụ cho việc kinh doanh, đến khi mặt nước cách mép trên của thành bể \(0,2\,{\rm{m}}\) thì ông dừng lại, và giá tiền nước là 15 000 đồng/m3. Khi đó số tiền nước mà ông An phải trả là 20 400 000 đồng.
Ông An xây một bể bơi, ban đầu có dạng là hình hộp chữ nhật \(ABCD.A'B'C'D'\). Sau đó ông làm lại mặt đáy như hình vẽ.

Biết rằng \(A'B'MN\) và \(MNEF\) là các hình chữ nhật, \(\left( {MNEF} \right){\rm{//}}\left( {A'B'C'D'} \right)\), \(AB = 20\,{\rm{m}}\), \(AD = 50\,{\rm{m}}\), \(AA' = 1,8\,{\rm{m}}\), \(MF = 30\,{\rm{m}}\), \(DE = 1,5\,{\rm{m}}\).
a) Cạnh BC của thành bể vuông góc với đường thẳng chứa MN của đáy bể.
b) Góc giữa thành bể \[ABB'A'\] và mặt phẳng chứa phần đáy \[\left( {MNA'B'} \right)\] gần bằng \(65^\circ 45'\).
c) Khoảng cách từ điểm B của góc bể đến mặt phẳng chứa phần đáy \[\left( {MNA'B'} \right)\] xấp xỉ bằng \(1,6599\,\,{\rm{m}}\).
d) Ông An bơm nước vào bể để phục vụ cho việc kinh doanh, đến khi mặt nước cách mép trên của thành bể \(0,2\,{\rm{m}}\) thì ông dừng lại, và giá tiền nước là 15 000 đồng/m3. Khi đó số tiền nước mà ông An phải trả là 20 400 000 đồng.
Quảng cáo
Trả lời:
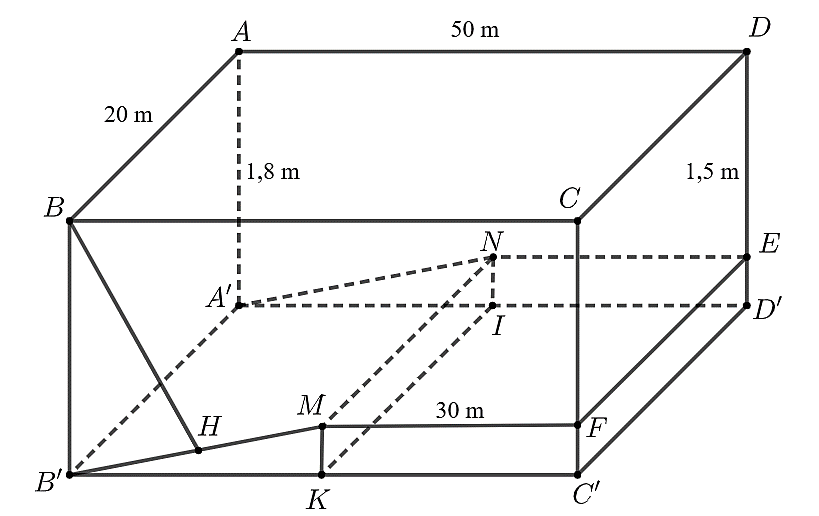
Ta có \(MN\,{\rm{//}}\,A'B'\) (do \(A'B'MN\) là hình chữ nhật).
Lại có \(A'B' \bot \left( {BCC'B'} \right)\), suy ra \(MN \bot \left( {BCC'B'} \right)\,\, \Rightarrow \,\,MN \bot BC\).
Ta có \[\left( {ABB'A'} \right) \cap \left( {MNA'B'} \right) = A'B'\], \[BB' \bot A'B',\,B'M \bot A'B'\].
Do đó, góc giữa thành bể \[ABB'A'\] và mặt phẳng chứa phần đáy \[\left( {MNA'B'} \right)\] là \(\widehat {BB'M}\).
Kẻ \(MK \bot B'C'\) tại K. Ta có \(MK = FC' = 1,8 - 1,5 = 0,3\,\,({\rm{m)}}\); \(B'K = 50 - 30 = 20\,\,({\rm{m)}}\).
Do đó, \(\tan \widehat {MB'K} = \frac{{MK}}{{B'K}} = \frac{{0,3}}{{20}} = \frac{3}{{200}}\).
Suy ra \(\widehat {MB'K} \approx 0^\circ 52'\,\, \Rightarrow \,\,\widehat {BB'M} \approx 90^\circ - 0^\circ 52' = 89^\circ 8'\).
Kẻ \(BH \bot B'M\) tại H. Khi đó BH là khoảng cách từ B đến mặt phẳng \[\left( {MNA'B'} \right)\].
Ta có \(BH = BB' \cdot \sin \widehat {BB'H} = 1,8 \cdot \sin 89^\circ 8' \approx 1,79979\,\,{\rm{(m)}}\).
Thể tích của bể ban đầu khi chưa làm phần đáy là \({V_{ABCD.A'B'C'D'}} = 20 \cdot 50 \cdot 1,8 = 1800\,\,({{\rm{m}}^{\rm{3}}})\).
Thể tích của phần đáy khi làm lại là \({V_{MFC'B'.NED'A'}} = \left( {30 + 50} \right) \cdot \frac{{0,3}}{2} \cdot 20 = 240\,\,{\rm{(}}{{\rm{m}}^{\rm{3}}})\).
Nếu bơm nước đến khi mặt nước cách mép trên của thành bể \(0,2\,{\rm{m}}\) dừng lại thì thể tích phần không có nước phía trên là \({V_0} = 20 \cdot 50 \cdot 0,2 = 200\,\,({{\rm{m}}^{\rm{3}}})\).
Thể tích nước là \(V = 1800 - 240 - 200 = 1\,360\,\,{\rm{(}}{{\rm{m}}^{\rm{3}}}{\rm{)}}\).
Số tiền nước ông An phải trả là \(1\,360 \cdot 15\,000 = 20\,400\,000\,\)(đồng).
Đáp án: a) Đúng, b) Sai, c) Sai, d) Đúng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
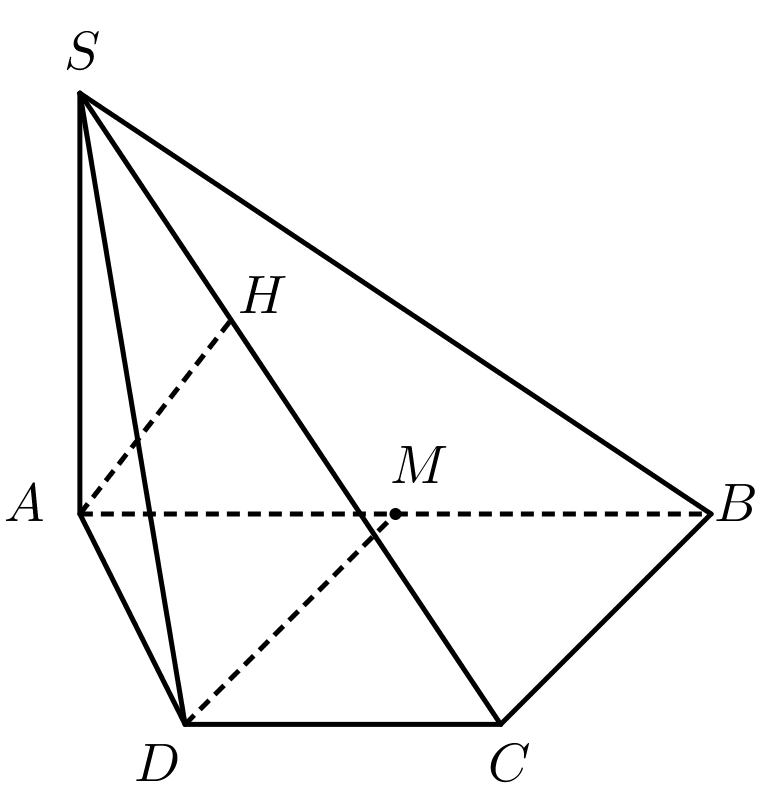
Ta có \[M\] là trung điểm của \[AB\].
Theo giả thiết suy ra \[ABCD\] là nửa lục giác đều nội tiếp đường tròn đường kính \[AB\]\[ \Rightarrow \left\{ \begin{array}{l}\widehat {ACB} = 90^\circ ;\widehat {ABC} = 60^\circ \\AC = \sqrt 3 \end{array} \right.\].
Vì \[DM{\rm{//}}BC \Rightarrow DM{\rm{//}}\left( {SBC} \right)\].
Do đó \[d\left( {DM,SB} \right) = d\left( {DM,\left( {SBC} \right)} \right) = d\left( {M,\left( {SBC} \right)} \right) = \frac{1}{2}d\left( {A,\left( {SBC} \right)} \right)\] (vì \[MB = \frac{1}{2}AB\]).
Kẻ \[AH \bot SC\] tại \[H\]. Ta có \[\left\{ \begin{array}{l}BC \bot AC\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAC} \right)\]\[ \Rightarrow AH \bot BC\].
Khi đó \[\left\{ \begin{array}{l}AH \bot SC\\AH \bot BC\end{array} \right. \Rightarrow AH \bot \left( {SBC} \right) \Rightarrow d\left( {A,\left( {SBC} \right)} \right) = AH\].
Xét tam giác \[SAC\] vuông tại \[A\], ta có \[A{H^2} = \frac{{A{C^2} \cdot S{A^2}}}{{A{C^2} + S{A^2}}} = \frac{{{{\left( {\sqrt 3 } \right)}^2} \cdot {3^2}}}{{{{\left( {\sqrt 3 } \right)}^2} + {3^2}}} = \frac{9}{4}\]\[ \Rightarrow AH = \frac{3}{2}\].
Vậy \[d\left( {DM,SB} \right) = \frac{1}{2}d\left( {A,\left( {SBC} \right)} \right) = \frac{1}{2}AH = \frac{3}{4} = 0,75\].
Lời giải
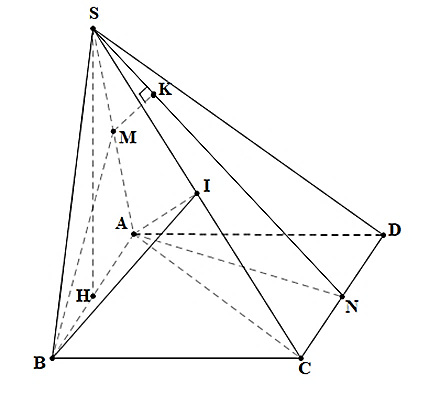
Vì tam giác \(SAB\) đều nên \(SH \bot AB\).
Mà \(\left( {SAB} \right) \bot \left( {ABCD} \right)\) nên \(SH \bot \left( {ABCD} \right)\).
Tam giác \(SAB\) đều cạnh \(a \Rightarrow SH = \frac{{a\sqrt 3 }}{2}\).
Diện tích hình thoi \(ABCD\):
\({S_{ABCD}} = 2{S_{\Delta ABC}} = 2 \cdot \frac{1}{2}AB \cdot BC \cdot \sin B = \frac{{{a^2}\sqrt 3 }}{2}\).
Vậy thể tích khối chóp \(S.ABCD\): \({V_{S.ABCD}} = \frac{1}{3}SH \cdot {S_{ABCD}} = \frac{1}{3} \cdot \frac{{a\sqrt 3 }}{2} \cdot \frac{{{a^2}\sqrt 3 }}{2} = \frac{{{a^3}}}{4}\).
Dễ thấy \(\Delta ABC\) đều \( \Rightarrow AC = BC = a \Rightarrow \)các tam giác \(SAC\) và \(SBC\) lần lượt cân tại \(A\) và \(B\).
Gọi \(I\) là trung điểm của \(SC \Rightarrow \left\{ \begin{array}{l}SC \bot AI\\SC \bot BI.\end{array} \right.\)
Suy ra \(\widehat {AIB}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {A,SC,B} \right]\).
Ta có \(S{C^2} = S{H^2} + C{H^2} = \frac{{3{a^2}}}{2} \Rightarrow S{I^2} = I{C^2} = \frac{{3{a^2}}}{8}\).
Suy ra \(I{A^2} = S{A^2} - S{I^2} = \frac{{5{a^2}}}{8}\). Tương tự \(I{B^2} = \frac{{5{a^2}}}{8}\).
Do đó \(\cos \alpha = \cos \widehat {AIB} = \frac{{I{A^2} + I{B^2} - A{B^2}}}{{2 \cdot IA \cdot IB}} = \frac{1}{5}\).
Ta có \(\Delta ACD\)đều \( \Rightarrow AN \bot CD \Rightarrow AN \bot AB \Rightarrow AN \bot \left( {SAB} \right) \Rightarrow \left( {SAN} \right) \bot \left( {SAB} \right)\).
\(\Delta SAB\) đều \( \Rightarrow BM \bot SA \Rightarrow BM \bot \left( {SAN} \right)\).
Dựng \(MK \bot SN\) tại \(K \Rightarrow MK\) là đoạn vuông góc chung của \(BM\) và \(SN\).
Suy ra \(MK = d\left( {BM,SN} \right)\).
Ta có \(MK = MS \cdot \sin \widehat {MSK} = MS \cdot \frac{{AN}}{{SN}} = MS \cdot \frac{{AN}}{{\sqrt {S{A^2} + A{N^2}} }} = \frac{a}{2} \cdot \frac{{\frac{{a\sqrt 3 }}{2}}}{{\sqrt {{a^2} + {{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}} }} = \frac{{a\sqrt {21} }}{{14}}\).
Vậy \(d\left( {BM,SN} \right) = \frac{{a\sqrt {21} }}{{14}}\).
Đáp án: a) Đúng, b) Sai, c) Sai, d) Đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.