Câu hỏi:

19/06/2025 8

Cho tam giác ABC có ba góc nhọn, đường cao AH. Ở miền ngoài của tam giác ABC vẽ các tam giác vuông cân ABE và ACF và tam giác ACF đều nhận A làm đỉnh góc vuông. Kẻ EM, FN cùng vuông góc với AH (M, N thuộc AH).

a) Chứng mình rằng: EM + HC = NH.

b) Chứng minh rằng: EN // FM.

Xem lời giải

Câu hỏi trong đề: 10000 câu trắc nghiệm tổng hợp môn Toán 2025 mới nhất (có đáp án) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Lời giải:

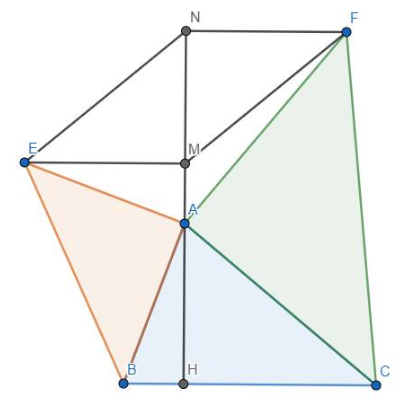
Chứng mình rằng: EM + HC = NH. (ảnh 1)

a) Do tam giác AEB vuông cân tại A nên \[\widehat {EAB} = 90^\circ ,\] AE = AB.

Ta thấy \[\widehat {MEA} = \widehat {BAH}\] vì cùng phụ với \[\widehat {EAM}\].

Xét hai tam giác HAB vuông tại H và MEA vuông tại M, ta có:

AE = AB (cmt)

\[\widehat {EAM} = \widehat {BAH}\]

Suy ra ∆HAB = ∆MEA

Suy ra AH = ME (1)

Tương tự ∆HAC = ∆NFA, suy ra HC = AC (2)

Từ (1) và (2) suy ra EM + HC = AH + AN hay EM + HC = HN

b) Từ ∆HAC = ∆NFA, suy ra AH = NF

Từ đó suy ra ME = NF (= AH)

Xét ∆MNE và ∆NMF ta có:

ME = NF, \[\widehat {EMN} = \widehat {FNM}\left( { = 90^\circ } \right)\], MN là cạnh chung

Suy ra ∆MNE = ∆NMF (c.g.c)

Suy ra \[\widehat {ENM} = \widehat {FMN}\]

Suy ra EN // FM (2 góc so le trong bằng nhau).

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Diện tích một trang của một cuốn sách là 600 cm². Do yêu cầu kĩ thuật, cần để lề trên và lề dưới là 3 cm, lề tráo và lề phải là 2 cm. Tính chiều dài của trang giấy để diện tích phần chữ in vào cuốn sách được nhiều nhất?

Xem đáp án

Lời giải

Lời giải:

Gọi chiều dài và chiều rộng của trang sách là x và y (cm). Ta có diện tích trang sách là xy = 600.

Do có lề trên và lề dưới là 3 cm, lề trái và lề phải là 2 cm, diện tích phần chữ in là (x ‒ 4)(y ‒ 6)

Từ xy = 600, ta có \[y = \frac{{600}}{x}.\] Thay vào diện tích phần chữ in, ta được:

\[S\left( x \right) = \left( {x - 4} \right)\left( {\frac{{600}}{x} - 6} \right) = 600 - 6x - \frac{{2400}}{x} + 24 = - 6x - \frac{{2400}}{x} + 624\]

Để diện tích phần chữ in lớn nhất, ta tìm đạo hàm của S(x) và cho bằng 0

\[S'\left( x \right) = - 6 + \frac{{2400}}{{{x^2}}} = 0\]

x² = 400

Suy ra x = 20 (vì x > 0)

Thay x = 20 và \[y = \frac{{600}}{x}\] ta được y = 30 cm.

Chiều dài trang giấy là x = 20 cm.

Câu 2

Rút gọn biểu thức sau \[A = \frac{{\sin 3x - \sin x}}{{2{{\cos }^2}x - 1}}\]

Xem đáp án

Lời giải

Lời giải:

Áp dụng công thức sin a – sin b = \[2cos\frac{{a + b}}{2}\sin \frac{{a - b}}{2}\]

Nên sin3x – sinx = \[2\cos \frac{{3x + x}}{2}\sin \frac{{3x - x}}{2}\]

= 2cos2x. sin x

Mà cos2x =\[2{\cos ^2}x - 1\]

Suy ra \[A = \frac{{\sin 3x - \sin x}}{{2{{\cos }^2}x - 1}}\]

\[ = \frac{{2cos2x.{\rm{ }}sin{\rm{ }}x}}{{\cos 2x}}\]= 2sinx

Câu 3