Câu hỏi:

19/06/2025 33

Cho tam giác ABC đều cạnh a, M là trung điểm của BC. Tính \[\overrightarrow {CA} - \overrightarrow {MC} .\]

Xem lời giải

Câu hỏi trong đề: 10000 câu trắc nghiệm tổng hợp môn Toán 2025 mới nhất (có đáp án) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Lời giải:

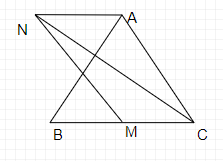
cho tam giác abc đều cạnh a m là trung điểm của bc tí ca-mc (ảnh 1)

Ta có \[\overrightarrow {CA} - \overrightarrow {MC} = \overrightarrow {CA} + \overrightarrow {CM} = \widehat {CN}\] với MN // AC; MN = AC; AN = MC

Suy ra tứ giác MNAC là hình bình hành.

\[\widehat {CMN} = 120^\circ \left( {MN//AC;\widehat {ACM} = 60^\circ } \right)\]

\[{\rm{cos}}\widehat {CMN} = \frac{{M{N^2} + M{C^2} - C{N^2}}}{{2 \cdot MN \cdot MC}} = \frac{{ - 1}}{2}\]

Suy ra \[\frac{{{a^2} + \frac{{{a^2}}}{4} - C{N^2}}}{{{a^2}}} = - \frac{1}{2}\]

\[C{N^2} = {a^2} + \frac{{{a^2}}}{4} + \frac{{{a^2}}}{2} = \frac{{7{a^2}}}{4}\] nên \[CN = a\frac{{\sqrt 7 }}{2}\]

Do đó \[{\rm{cos}}\widehat {NCM} = \frac{{N{C^2} + C{M^2} - N{M^2}}}{{2 \cdot NC \cdot CM}} = \frac{{\frac{{7{a^2}}}{4} + \frac{{{a^2}}}{4} - {a^2}}}{{{a^2}\frac{{\sqrt 7 }}{2}}} = \frac{2}{{\sqrt 7 }}.\]

Vậy \[\overrightarrow {CA} - \overrightarrow {MC} .\]

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Bánh xe đạp có đường kính 55 cm (kể cả lốp). Nếu chạy với vận tốc 40 km/h thì trong 25 s bánh xe quay được số vòng bằng bao nhiêu?

Xem đáp án

Lời giải

Lời giải:

Đổi 40 km/h = \[\frac{{100}}{9}\]m/s

Chu vi của bánh xe đạp là:

C = D × π = 55π (cm)

Quãng đường xe đạp đi được trong 25 s là:

1 009 × 25 = 25 009 (m)

Với tốc độ 40 km/h thì trong 25 s bánh xe quay được số vòng là:

25 009 : 0,55π ≈ 160,8 (vòng)

Đáp số: 160,8 vòng

Câu 2

Diện tích một trang của một cuốn sách là 600 cm². Do yêu cầu kĩ thuật, cần để lề trên và lề dưới là 3 cm, lề tráo và lề phải là 2 cm. Tính chiều dài của trang giấy để diện tích phần chữ in vào cuốn sách được nhiều nhất?

Xem đáp án

Lời giải

Lời giải:

Gọi chiều dài và chiều rộng của trang sách là x và y (cm). Ta có diện tích trang sách là xy = 600.

Do có lề trên và lề dưới là 3 cm, lề trái và lề phải là 2 cm, diện tích phần chữ in là (x ‒ 4)(y ‒ 6)

Từ xy = 600, ta có \[y = \frac{{600}}{x}.\] Thay vào diện tích phần chữ in, ta được:

\[S\left( x \right) = \left( {x - 4} \right)\left( {\frac{{600}}{x} - 6} \right) = 600 - 6x - \frac{{2400}}{x} + 24 = - 6x - \frac{{2400}}{x} + 624\]

Để diện tích phần chữ in lớn nhất, ta tìm đạo hàm của S(x) và cho bằng 0

\[S'\left( x \right) = - 6 + \frac{{2400}}{{{x^2}}} = 0\]

x² = 400

Suy ra x = 20 (vì x > 0)

Thay x = 20 và \[y = \frac{{600}}{x}\] ta được y = 30 cm.

Chiều dài trang giấy là x = 20 cm.

Câu 3