Một bể nước hình nón ngược với bán kính đáy bằng 2 m và chiều cao bằng 4 m (tham khảo hình vẽ dưới đây). Nước được bơm vào bể với tốc độ không đổi là 2 m3/phút. Hỏi tốc độ dâng lên của mực nước (đơn vị m/phút) bằng bao nhiêu khi mực nước trong bể đạt độ sâu bằng 3 m (làm tròn kết quả đến chữ số hàng phần trăm)?
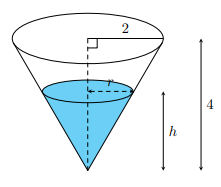
Một bể nước hình nón ngược với bán kính đáy bằng 2 m và chiều cao bằng 4 m (tham khảo hình vẽ dưới đây). Nước được bơm vào bể với tốc độ không đổi là 2 m3/phút. Hỏi tốc độ dâng lên của mực nước (đơn vị m/phút) bằng bao nhiêu khi mực nước trong bể đạt độ sâu bằng 3 m (làm tròn kết quả đến chữ số hàng phần trăm)?

Quảng cáo
Trả lời:
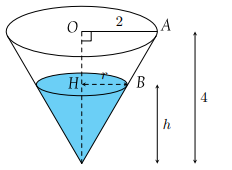
Ta có: \[\frac{h}{4} = \frac{r}{2}\] hay \[r = \frac{h}{2}\]
Suy ra \[V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi \cdot {\left( {\frac{h}{2}} \right)^2} \cdot h = \frac{1}{{12}}\pi \cdot {h^3}\].
Ta có \[\frac{{dV}}{{dt}}\] là tốc độ bơm nước vào bể theo thời gian;
\[\frac{{dh}}{{dt}}\] là tốc độ dâng lên của nước theo thời gian.
Suy ra \[\frac{{dV}}{{dt}} = \frac{{3\pi {h^2}}}{{12}} \cdot \frac{{dh}}{{dt}}\]
\[\frac{{dh}}{{dt}} = \frac{{dV}}{{dt}}:\frac{{3\pi {h^2}}}{{12}} = 2 \cdot \frac{{12}}{{3\pi {h^2}}}\]
Tại thời điểm h = 3
\[\frac{{dh}}{{dt}} = \frac{{24}}{{3\pi \cdot {3^2}}} = 0,28\] (m/phút).
Vậy tốc độ dâng lên của mực nước là 0,28 m/phút.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải:
Đổi 40 km/h = \[\frac{{100}}{9}\]m/s
Chu vi của bánh xe đạp là:
C = D × π = 55π (cm)
Quãng đường xe đạp đi được trong 25 s là:
1 009 × 25 = 25 009 (m)
Với tốc độ 40 km/h thì trong 25 s bánh xe quay được số vòng là:
25 009 : 0,55π ≈ 160,8 (vòng)
Đáp số: 160,8 vòng
Lời giải
Lời giải:
Gọi chiều dài và chiều rộng của trang sách là x và y (cm). Ta có diện tích trang sách là xy = 600.
Do có lề trên và lề dưới là 3 cm, lề trái và lề phải là 2 cm, diện tích phần chữ in là (x ‒ 4)(y ‒ 6)
Từ xy = 600, ta có \[y = \frac{{600}}{x}.\] Thay vào diện tích phần chữ in, ta được:
\[S\left( x \right) = \left( {x - 4} \right)\left( {\frac{{600}}{x} - 6} \right) = 600 - 6x - \frac{{2400}}{x} + 24 = - 6x - \frac{{2400}}{x} + 624\]
Để diện tích phần chữ in lớn nhất, ta tìm đạo hàm của S(x) và cho bằng 0
\[S'\left( x \right) = - 6 + \frac{{2400}}{{{x^2}}} = 0\]
x2 = 400
Suy ra x = 20 (vì x > 0)
Thay x = 20 và \[y = \frac{{600}}{x}\] ta được y = 30 cm.
Chiều dài trang giấy là x = 20 cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.