2.1. Tính giá trị của biểu thức \(A = \frac{{x - 2y - z}}{2}\) với \(x = - 1;y = 1;z = - 1\).
2.2. Cho đa thức \(A\left( x \right) = \frac{3}{4}{x^3} - 1 + \frac{3}{5}x + 4{x^2} + \frac{5}{4}{x^3} - \frac{8}{5}x + 4 + 7{x^2}\).
a) Thu gọn và sắp xếp đa thức \(A\left( x \right)\) theo lũy thừa giảm dần của biến.
b) Tính giá trị của \(A\left( x \right)\) tại \(x = - 1\).
c) Tìm đa thức \(C\left( x \right)\) sao cho \(B\left( x \right) - C\left( x \right) = A\left( x \right)\), biết \(B\left( x \right) = 2{x^3} + 12{x^2} - 3x + 3\). Tìm nghiệm của đa thức \(C\left( x \right)\).
2.1. Tính giá trị của biểu thức \(A = \frac{{x - 2y - z}}{2}\) với \(x = - 1;y = 1;z = - 1\).
2.2. Cho đa thức \(A\left( x \right) = \frac{3}{4}{x^3} - 1 + \frac{3}{5}x + 4{x^2} + \frac{5}{4}{x^3} - \frac{8}{5}x + 4 + 7{x^2}\).
a) Thu gọn và sắp xếp đa thức \(A\left( x \right)\) theo lũy thừa giảm dần của biến.
b) Tính giá trị của \(A\left( x \right)\) tại \(x = - 1\).
c) Tìm đa thức \(C\left( x \right)\) sao cho \(B\left( x \right) - C\left( x \right) = A\left( x \right)\), biết \(B\left( x \right) = 2{x^3} + 12{x^2} - 3x + 3\). Tìm nghiệm của đa thức \(C\left( x \right)\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
2.1. Thay \(x = - 1;y = 1;z = - 1\) vào biểu thức \(A = \frac{{x - 2y - z}}{2}\), ta được:
\(A = \frac{{ - 1 - 2.1 - \left( { - 1} \right)}}{2} = \frac{{ - 1 - 2 + 1}}{2} = - 1\).
Vậy giá trị của biểu thức \(A = - 1\).
2.2. a) \(A\left( x \right) = \frac{3}{4}{x^3} - 1 + \frac{3}{5}x + 4{x^2} + \frac{5}{4}{x^3} - \frac{8}{5}x + 4 + 7{x^2}\)
\( = \left( {\frac{3}{4} + \frac{5}{4}} \right){x^3} + \left( {4 + 7} \right){x^2} + \left( {\frac{3}{5} - \frac{8}{5}} \right)x - 1 + 4\)
\( = 2{x^3} + 11{x^2} - x + 3\).
b) Thay \(x = - 1\) vào \(A\left( x \right)\), ta được: \(A\left( { - 1} \right) = 2.{\left( { - 1} \right)^3} + 11.{\left( { - 1} \right)^2} - \left( { - 1} \right) + 3 = - 2 + 11 + 1 + 3 = 13\).
Vậy giá trị của \(A = 13\) khi \(x = - 1\).
c) Ta có \(B\left( x \right) - C\left( x \right) = A\left( x \right)\).
Suy ra \(C\left( x \right) = B\left( x \right) - A\left( x \right)\)
\( = 2{x^3} + 12{x^2} - 3x + 3 - \left( {2{x^3} + 11{x^2} - x + 3} \right)\)
\( = 2{x^3} + 12{x^2} - 3x + 3 - 2{x^3} - 11{x^2} + x - 3\)
\( = {x^2} - 2x\).
Để tìm nghiệm của đa thức \(C\left( x \right)\), ta cho \(C\left( x \right) = 0\)
Do đó \({x^2} - 2x = 0\) hay \(x\left( {x - 2} \right) = 0\)
Suy ra \(x = 0\) hoặc \(x = 2\).
Vậy nghiệm của đa thức \(C\left( x \right)\) là \(x \in \left\{ {0;2} \right\}\).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
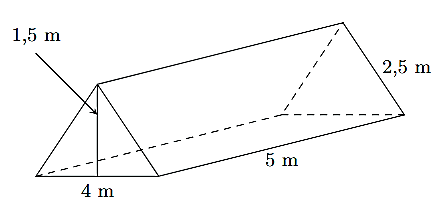
a) Thể tích khoảng không bên trong lều là: \(\frac{1}{2}.1,5.4.5 = 15{\rm{ }}\left( {{{\rm{m}}^3}} \right)\).
b) Diện tích bạt cần để dựng lều là tổng diện tích hai mặt bên và hai mặt đáy của hình lăng trụ đứng tam giác.
Do đó, diện tích bạt cần dùng để dựng lều là: \(2.2,5.5 + 2.\frac{1}{2}.1,5.4 = 31{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
Lời giải
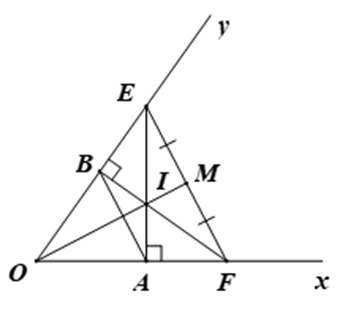
a) Xét \(\Delta OAE\) và \(\Delta OBF\), có:
\(\widehat {OAE} = \widehat {OBF} = 90^\circ \)
\(OA = OB\) (giả thiết)
\(\widehat {AOB}\) là góc chung
Do đó, \(\Delta OAE = \Delta OBF\) (cgv – gn)
Suy ra \(OE = OF\) (hai cạnh tương ứng)
b) Áp dụng bất đẳng thức tam giác cho \(\Delta EIF\), ta được: \(EF < EI + IF\).
Mà \(2EM = EF\) (do \(M\) là trung điểm của \(EF\))
Suy ra \(2EM < EI + IF.\)
Vậy \(EM < \frac{{EI + IF}}{2}.\)
c) Xét \(\Delta EOF\) có hai đường cao \(FB\) và \(AE\) cắt nhau tại \(I\).
Suy ra \(I\) là trực tâm của \(\Delta OEF.\)
Do đó, \(OI \bot EF\) (1)
Xét \(\Delta OEM\) và \(\Delta OFM\), có:
\(OM\) là cạnh chung
\(ME = MF\) (do \(M\) là trung điểm của \(EF\))
\(OE = OF\) (câu a)
Do đó, \(\Delta OEM = \Delta OFM\) (c.c.c)
Suy ra \(\widehat {OME} = \widehat {OMF}\) (hai góc tương ứng)
Mà \(\widehat {OME} + \widehat {OMF} = 180^\circ \) (hai góc kề bù)
Do đó, \(\widehat {OME} = \widehat {OMF} = 90^\circ \) hay \(OM \bot EF\) (2)
Từ (1) và (2) suy ra \(O,I,M\) thẳng hàng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo