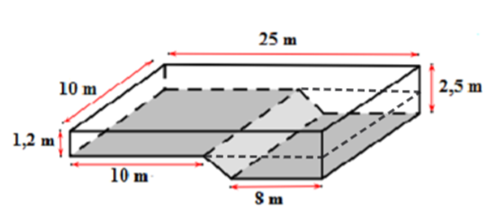
Một bể bơi được xây dựng thành hai khu vực với độ sâu khác nhau cho người lớn và trẻ em. Các kích thước của lòng bể được cho như hình vẽ bên.

     a) Tính thể tích của bể bơi.

     b) Người ta dùng một máy bơm để bơm đầy nước vào bể. Biết cứ sau mỗi phút máy bơm bơm được \(500\) lít nước. Hỏi sau bao lâu bể bơi được bơm đầy?

a) Xét \(\Delta ABC\) vuông tại \(A\) có \(\widehat B = 60^\circ \)

Suy ra \(\widehat C = 90^\circ - \widehat B = 30^\circ \).

Do đó \(\widehat C < \widehat B\) nên \(AB < AC\) nên \(M\) nằm giữa \(H\) và \(C\)

Hay \(HM < HC\)

Mà \(HM = HB\), suy ra \(HB < HC\).

b) Xét \(\Delta AHB\) và \(\Delta AHM\) có:

\(\widehat {AHB} = \widehat {AHM} = 90^\circ \);

\(AH\) là cạnh chung;

\(HM = HB\) (giả thiết).

Do đó \(\Delta AHB = \Delta AHM\) (hai cạnh góc vuông)

Suy ra \(AB = AM\) (hai cạnh tương ứng)

\(\Delta ABM\) có \(AB = AM\) nên là tam giác cân tại \(A\).

Lại có \(\widehat B = 60^\circ \) (giả thiết) nên \(\Delta ABM\) là tam giác đều.

c) Do \(\Delta ABM\) là tam giác đều nên \(\widehat {MAB} = 60^\circ \).

Suy ra \(\widehat {MAC} = 90^\circ - \widehat {MAB} = 90^\circ - 60^\circ = 30^\circ \)

Tam giác \(MAC\) có \(\widehat {MAC} = \widehat {MCA} = 30^\circ \) nên là tam giác cân tại \(M\).

Suy ra \(MA = MC\).

Lại có \(MA = MB\) (do \(\Delta ABM\) đều)

Do đó \(MB = MC\) hay \(M\) là trung điểm của \(BC\).

Xét \(\Delta ABC\) có \(AM,BN\) là hai đường trung tuyến của tam giác cắt nhau tại \(O\) nên \(O\) là trọng tâm của tam giác.

Suy ra \(AO = \frac{2}{3}AM = \frac{2}{3}AB = \frac{2}{3}.6 = 4\,\,\left( {{\rm{cm}}} \right)\).

Gọi số tiền thưởng của Tài, Trí, Đức lần lượt là \(x,y,z\) (\(x,y,z > 0,\) đồng).

Theo bài ra ta có: \(\frac{x}{5} = \frac{y}{3}\) và \(z = 25\% \left( {x + y} \right)\) suy ra \(x + y = 4z\).

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có: \(\frac{x}{5} = \frac{y}{3} = \frac{{x + y}}{8} = \frac{{4z}}{8} = \frac{z}{2}\).

Suy ra \(\frac{x}{5} = \frac{y}{3} = \frac{z}{2}\).

Mà, theo đề \(x + y + z = 100{\rm{ }}000\).

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có: \(\frac{x}{5} = \frac{y}{3} = \frac{z}{2} = \frac{{x + y + z}}{{5 + 3 + 2}} = \frac{{100{\rm{ }}000}}{{10}} = 10{\rm{ }}000\).

Suy ra \(x = 50{\rm{ }}000;{\rm{ }}y = 30{\rm{ }}000;{\rm{ }}z = 20{\rm{ }}000\).

Vậy số tiền thưởng của ba bạn Tài, Trí, Đức lần lượt là \(50{\rm{ }}000\) đồng, \(30{\rm{ }}000\) đồng và \(20{\rm{ }}000\) đồng.