(1,5 điểm) Cho tam giác \(ABC\). Gọi \(D\) và \(E\) là hai điểm trên cạnh \(BC\) sao cho ba cạnh\(BD = DE = EC.\) Vẽ đường trung tuyến \(AO\) của tam giác \(ABC\). Trên tia đối của tia \(OA\) lấy điểm \(F\) sao cho \(OF = OA.\)
a) Chứng minh \(D\) là trọng tâm của tam giác \(BAF\); \(E\) là trọng tâm của tam giác \(CAF.\)
b) Tia \(AD\) cắt \(BF\) tại \(N,\) tia \(FE\) cắt \(AC\) tại \(M.\) Chứng minh ba điểm \(M,O,N\) thẳng hàng.
Quảng cáo
Trả lời:
Hướng dẫn giải
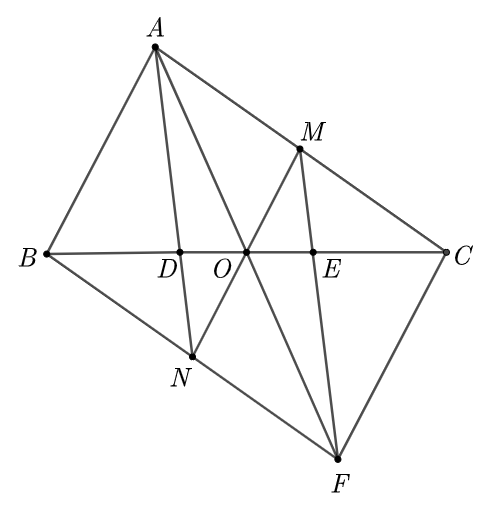
Vì \(AD\) cắt \(BF\) tại \(N\) nên \(FN = BN = \frac{1}{2}BF\) (1).
Chứng minh tương tự, ta được: \(AM = MC = \frac{1}{2}AC\) (2)
Vì \(OA\) là đường tủng tuyến của tam giác \(ABC\) nên \(O\) là trung điểm của \(BC\) hay \(OB = OC\).
Xét \(\Delta OFB\) và \(\Delta OAC\) có:
\(OF = OA\) (gt)
\(\widehat {FOB} = \widehat {AOC}\) (hai góc đối đỉnh)
\(OB = OC\) (cmt)
Do đó, \(\Delta OFB = \Delta OAC\) (c.g.c)
Suy ra \(\widehat {OFB} = \widehat {OAC}\) (hai góc tương ứng) và \(BF = AC\) (hai cạnh tương ứng) (3)
Từ (1), (2) và (3) suy ra \(AM = FN\).
Xét \(\Delta AOM\) và \(\Delta FON\) có:
\(AM = FN\) (cmt)
\(\widehat {OFN} = \widehat {OAM}\) (cmt)
\(OF = OA\) (gt)
Do đó, \(\Delta AOM = \Delta FON\) (c.g.c)
Suy ra \(\widehat {AOM} = \widehat {FON}\) (hai góc tương ứng)
Mà \(\widehat {AOM} + \widehat {FOM} = 180^\circ \) (hai góc kề bù)
Suy ra \(\widehat {FON} + \widehat {FOM} = 180^\circ \).
Do đó, \(M,O,N\) thẳng hàng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Từ tỉ lệ thức \(\frac{a}{c} = \frac{c}{b}\) suy ra \({c^2} = ab\) (1)
Đặt \(\frac{a}{c} = \frac{c}{b} = k\) suy ra \(a = ck;c = bk\). Do đó, \(\frac{{{a^2} + {c^2}}}{{{b^2} + {c^2}}} = \frac{{{{\left( {ck} \right)}^2} + {c^2}}}{{{b^2} + {{\left( {bk} \right)}^2}}} = \frac{{{c^2}\left( {{k^2} + 1} \right)}}{{{b^2}\left( {{k^2} + 1} \right)}} = \frac{{{c^2}}}{{{b^2}}}\) (2)
Từ (1) và (2) ta có: \(\frac{{{a^2} + {c^2}}}{{{b^2} + {c^2}}} = \frac{{{c^2}}}{{{b^2}}} = \frac{{ab}}{{{b^2}}} = \frac{a}{b}.\)
Suy ra \(\frac{{{b^2} + {c^2}}}{{{a^2} + {c^2}}} = \frac{b}{a}\), suy ra \(\frac{{{b^2} + {c^2}}}{{{a^2} + {c^2}}} - 1 = \frac{b}{a} - 1\) hay \(\frac{{{b^2} + {c^2} - {c^2} - {a^2}}}{{{a^2} + {c^2}}} = \frac{{b - a}}{a}\).
Do đó, \(\frac{{{b^2} - {a^2}}}{{{a^2} + {c^2}}} = \frac{{b - a}}{a}\) (đpcm).
Lời giải
Hướng dẫn giải
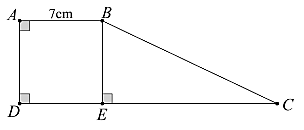
4.1. Ta có \(E\) là hình chiếu của \(B\) lên cạnh \(CD\), suy ra \(BE \bot CD\) tại \(E\) hay \(CE \bot BE\) tại \(E\).
Do đó, độ dài \(CE\) là khoảng cách từ \(C\) đến đường thẳng \(BE\) (1).
Hình vuông \(ABED\) có diện tích là \(7.7 = 49{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^2}} \right)\).
Diện tích hình thang \(ABCD\) là \(49.2 = 98{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\).
Ta có công thức tính diện tích hình thang \(ABCD\) là \(S = \frac{{\left( {AB + CD} \right).BE}}{2}\).
Mà \(AB = BE = 7{\rm{ cm; }}S = 98{\rm{ c}}{{\rm{m}}^2}\).
Suy ra, độ dài đáy lớn của hình thang \(ABCD\) là \(CD = \frac{{98.2}}{7} = 21{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^2}} \right)\).
Do \(E \in CD\) nên \(CD = CE + DE\).
Suy ra \(CE = CD - DE = 21 - 7 = 14{\rm{ }}\left( {{\rm{cm}}} \right)\) (2).
Từ (1) và (2) suy ra khoảng cách từ \(C\) đến đường thẳng \(BE\) là \(14{\rm{ }}\left( {{\rm{cm}}} \right)\).
4.2. Giả sử tam giác \(ABC\) có \(AB = 6{\rm{ cm, }}AC = 2{\rm{ cm}}{\rm{.}}\)
Theo bất đẳng thức tam giác, ta có \(AB - AC < BC < AB + AC\). Suy ra \(4 < BC < 8\).
Mà \(BC\) có độ dài là một số chẵn.
Do đó, \(BC = 6{\rm{ cm}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.