(1,5 điểm) Tìm \(x,y,z\) trong các tỉ lệ thức sau:
a) \(\frac{x}{3} = \frac{{2,5}}{{1,5}};\)
b) \(\frac{x}{{15}} = \frac{y}{7}\) và \(y - x = 16;\)
c) \(\frac{x}{2} = \frac{y}{3} = \frac{z}{5}\) và \(x - 2y + 3z = 38.\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
a) \(\frac{x}{3} = \frac{{2,5}}{{1,5}}\) suy ra \(1,5x = 2,5.3\), do đó \(x = \frac{{2,5.3}}{{1,5}} = 5\).
Vậy \(x = 5\).
b) \(\frac{x}{{15}} = \frac{y}{7}\) và \(y - x = 16\).
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{x}{{15}} = \frac{y}{7} = \frac{{y - x}}{{7 - 15}} = \frac{{16}}{{ - 8}} = - 2\).
Suy ra \(x = 15.\left( { - 2} \right) = - 30\) và \(y = 7.\left( { - 2} \right) = - 14\).
Vậy \(x = - 30\) và \(y = - 14\).
c) \(\frac{x}{2} = \frac{y}{3} = \frac{z}{5}\) và \(x - 2y + 3z = 38.\)
Ta có \(\frac{x}{2} = \frac{y}{3} = \frac{z}{5}\) hay \(\frac{x}{2} = \frac{{2y}}{6} = \frac{{3z}}{{15}}\).
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{x}{2} = \frac{{2y}}{6} = \frac{{3z}}{{15}} = \frac{{x - 2y + 3z}}{{2 + 6 + 15}} = \frac{{38}}{{23}}\).
Suy ra \(x = \frac{{76}}{{23}};y = \frac{{119}}{{23}};z = \frac{{190}}{{23}}\).
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
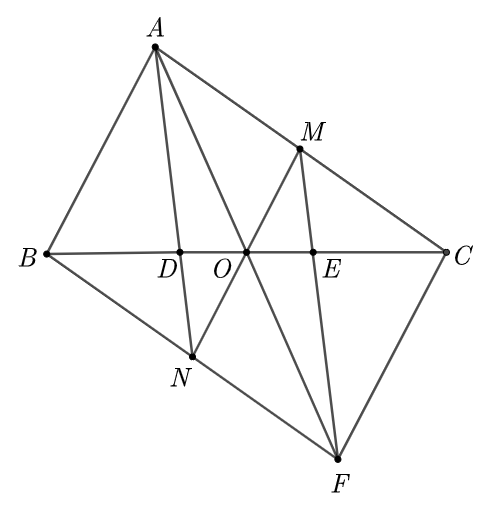
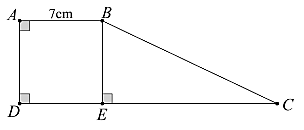
Vì \(AD\) cắt \(BF\) tại \(N\) nên \(FN = BN = \frac{1}{2}BF\) (1).
Chứng minh tương tự, ta được: \(AM = MC = \frac{1}{2}AC\) (2)
Vì \(OA\) là đường tủng tuyến của tam giác \(ABC\) nên \(O\) là trung điểm của \(BC\) hay \(OB = OC\).
Xét \(\Delta OFB\) và \(\Delta OAC\) có:
\(OF = OA\) (gt)
\(\widehat {FOB} = \widehat {AOC}\) (hai góc đối đỉnh)
\(OB = OC\) (cmt)
Do đó, \(\Delta OFB = \Delta OAC\) (c.g.c)
Suy ra \(\widehat {OFB} = \widehat {OAC}\) (hai góc tương ứng) và \(BF = AC\) (hai cạnh tương ứng) (3)
Từ (1), (2) và (3) suy ra \(AM = FN\).
Xét \(\Delta AOM\) và \(\Delta FON\) có:
\(AM = FN\) (cmt)
\(\widehat {OFN} = \widehat {OAM}\) (cmt)
\(OF = OA\) (gt)
Do đó, \(\Delta AOM = \Delta FON\) (c.g.c)
Suy ra \(\widehat {AOM} = \widehat {FON}\) (hai góc tương ứng)
Mà \(\widehat {AOM} + \widehat {FOM} = 180^\circ \) (hai góc kề bù)
Suy ra \(\widehat {FON} + \widehat {FOM} = 180^\circ \).
Do đó, \(M,O,N\) thẳng hàng.
Lời giải
Hướng dẫn giải
Từ tỉ lệ thức \(\frac{a}{c} = \frac{c}{b}\) suy ra \({c^2} = ab\) (1)
Đặt \(\frac{a}{c} = \frac{c}{b} = k\) suy ra \(a = ck;c = bk\). Do đó, \(\frac{{{a^2} + {c^2}}}{{{b^2} + {c^2}}} = \frac{{{{\left( {ck} \right)}^2} + {c^2}}}{{{b^2} + {{\left( {bk} \right)}^2}}} = \frac{{{c^2}\left( {{k^2} + 1} \right)}}{{{b^2}\left( {{k^2} + 1} \right)}} = \frac{{{c^2}}}{{{b^2}}}\) (2)
Từ (1) và (2) ta có: \(\frac{{{a^2} + {c^2}}}{{{b^2} + {c^2}}} = \frac{{{c^2}}}{{{b^2}}} = \frac{{ab}}{{{b^2}}} = \frac{a}{b}.\)
Suy ra \(\frac{{{b^2} + {c^2}}}{{{a^2} + {c^2}}} = \frac{b}{a}\), suy ra \(\frac{{{b^2} + {c^2}}}{{{a^2} + {c^2}}} - 1 = \frac{b}{a} - 1\) hay \(\frac{{{b^2} + {c^2} - {c^2} - {a^2}}}{{{a^2} + {c^2}}} = \frac{{b - a}}{a}\).
Do đó, \(\frac{{{b^2} - {a^2}}}{{{a^2} + {c^2}}} = \frac{{b - a}}{a}\) (đpcm).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo