(1,5 điểm) Cho hai đoạn thẳng \(AC\) và \(BD\) cắt nhau tại trung điểm \(O\) của mỗi đoạn. Gọi \(M,N\) lần lượt là trung điểm của \(BC,CD\). Đoạn thẳng \(AM,AN\) cắt \(BD\) lần lượt tại \(I,K\). Chứng minh:
a) \(I\) là trọng tâm của \(\Delta ABC\) và \(K\) là trọng tâm của tam giác \(\Delta ADC\).
b) \(BI = IK = KD.\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
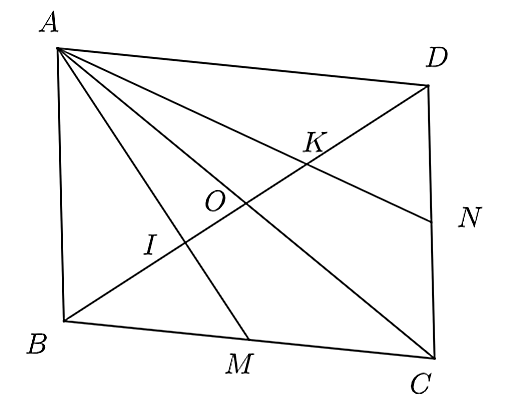
a) Xét \(\Delta ABC\), ta có: \(O\) là trung điểm của \(AC\), \(M\) là trung điểm của \(BC\).
Do đó, \(BO,AM\) là các đường trung tuyến của \(\Delta ABC\).
Mà \(BO\) cắt \(AM\) tại \(I\) nên \(I\) là trọng tâm của \(\Delta ABC\).
Xét \(\Delta ADC\), ta có: \(O\) là trung điểm của \(AC\), \(N\) là trung điểm của \(DC\).
Do đó, \(DO,AN\) là các đường trung tuyến của \(\Delta ADC\).
Mà \(DO\) cắt \(AN\) tại \(K\) nên \(K\) là trọng tâm của \(\Delta ADC\).
b) Xét \(\Delta ABC\) có \(I\) là trọng tâm nên \(IO = \frac{1}{3}BO\).
Xét \(\Delta ADC\) có \(K\) là trọng tâm nên \(KO = \frac{1}{3}DO\).
Mà \(O\) là trung điểm của \(BD\) nên \(BO = DO\).
Do đó, ta có: \(IO + KO = \frac{1}{3}BO + \frac{1}{3}DO = \frac{2}{3}BO\) hay \(IK = \frac{2}{3}BO\).
Do đó, \(BI = IK = KD = \frac{2}{3}BO = \frac{2}{3}DO.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
4.1.
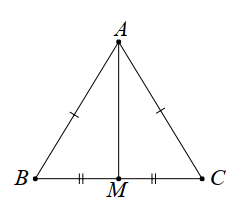
Xét
\(\Delta ABM\) và \(\Delta ACM\) có:
\(AB = AC\) (\(\Delta ABC\) cân tại \(A\))
\(\widehat B = \widehat C\)(\(\Delta ABC\) cân tại \(A\))
\(BM = MC\)
Suy ra \(\Delta ABM = \Delta ACM\) (c.g.c)
Do đó, \(\widehat {AMB} = \widehat {AMC}\) (hai góc tương ứng)
Mà hai góc \(\widehat {AMB} = \widehat {AMC}\) (hai góc tương ứng) (1)
Mà hai góc \(\widehat {AMB}\) và \(\widehat {AMC}\) là hai góc kề bù.
Suy ra \(\widehat {AMB} + \widehat {AMC} = 180^\circ \) (2)
Từ (1) và (2) suy ra \(\widehat {AMB} = \widehat {AMC} = \frac{{180^\circ }}{2} = 90^\circ \).
Do đó, \(AM \bot BC\) tại \(M.\)
Vậy \(AM\) là khoảng cách từ \(A\) đến cạnh \(BC\) của tam giác \(ABC.\)
4.2. Ta có \(BC > AB,BC > AC\) nên \(BC + BC + BC > AC + AB + BC\) tức là \(3BC > 18\) hay \(BC > 6.\)
Ta có \(BC < AC + AB\) nên \(BC + BC < AB + AC + BC\), tức là \(2BC < 18\) nên \(BC < 9\).
Từ đây suy ra \(6 < BC < 9\) và \(BC\) là một số tự nhiên chẵn nên \(BC = 8{\rm{ cm}}{\rm{.}}\)
Lời giải
Hướng dẫn giải
2.1. Có \(10\) vòi nước công suất như nhau cùng chảy vào một bể thì sau 6 giờ thì đầy bể. Vậy hỏi số vòi nước cùng công suất để sau 5 giờ thì đầy bể là bao nhiêu?
2.2.Gọi số cây mỗi lớp 7A, 7B, 7C trồng được lần lượt là \(a,b,c\) cây \(\left( {a,b,c \in {\mathbb{N}^*}} \right)\).
Số cây lớp 7A, 7B, 7C trồng lần lượt tỉ lệ với \(6;4;5\) suy ra \(\frac{a}{6} = \frac{b}{4} = \frac{c}{5}\).
Tổng số cây lớp 7B và 7C trồng được nhiều hơn của lớp 7A là \(15\) cây.
Do đó, ta có: \(b + c - a = 15\).
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có: \(\frac{a}{6} = \frac{b}{4} = \frac{c}{5} = \frac{{b + c - a}}{{4 + 5 - 6}} = \frac{{15}}{3} = 5\).
Ta có: \(a = 6.5 = 30\) (thỏa mãn), \(b = 5.4 = 20\) (thỏa mãn), \(c = 5.5 = 25\) (thỏa mãn)
Vậy số cây mỗi lớp 7A, 7B, 7C trồng được lần lượt là \(30\) cây, \(20\) cây, \(25\) cây.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập