Bộ 10 đề thi giữa kì 2 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 10

Hướng dẫn giải

a) \(\frac{{1,2}}{x} = \frac{5}{2}\) nên \(x = \frac{{2.1,2}}{5} = 0,48\). Vậy \(x = 0,48\).

b) \(\frac{x}{3} = \frac{y}{2}\) và \(x + y = 10\).

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có: \(\frac{x}{3} = \frac{y}{2} = \frac{{x + y}}{{3 + 2}} = \frac{{10}}{5} = 2\).

Suy ra \(x = 3.2 = 6;{\rm{ }}y = 2.2 = 4\).

Vậy \(x = 6;y = 4.\)

c) \(\frac{x}{3} = \frac{y}{4} = \frac{z}{6}\) và \(y + z = 80\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có: \(\frac{x}{3} = \frac{y}{4} = \frac{z}{6} = \frac{{y + z}}{{4 + 6}} = \frac{{80}}{{10}} = 8\).

Suy ra \(x = 3.8 = 24;{\rm{ }}y = 4.8 = 32;{\rm{ }}z = 6.8 = 48\).

Vậy \(x = 24;{\rm{ }}y = 32;{\rm{ }}z = 48.\)

Hướng dẫn giải

2.1. Có \(10\) vòi nước công suất như nhau cùng chảy vào một bể thì sau 6 giờ thì đầy bể. Vậy hỏi số vòi nước cùng công suất để sau 5 giờ thì đầy bể là bao nhiêu?

2.2.Gọi số cây mỗi lớp 7A, 7B, 7C trồng được lần lượt là \(a,b,c\) cây \(\left( {a,b,c \in {\mathbb{N}^*}} \right)\).

Số cây lớp 7A, 7B, 7C trồng lần lượt tỉ lệ với \(6;4;5\) suy ra \(\frac{a}{6} = \frac{b}{4} = \frac{c}{5}\).

Tổng số cây lớp 7B và 7C trồng được nhiều hơn của lớp 7A là \(15\) cây.

Do đó, ta có: \(b + c - a = 15\).

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có: \(\frac{a}{6} = \frac{b}{4} = \frac{c}{5} = \frac{{b + c - a}}{{4 + 5 - 6}} = \frac{{15}}{3} = 5\).

Ta có: \(a = 6.5 = 30\) (thỏa mãn), \(b = 5.4 = 20\) (thỏa mãn), \(c = 5.5 = 25\) (thỏa mãn)

Vậy số cây mỗi lớp 7A, 7B, 7C trồng được lần lượt là \(30\) cây, \(20\) cây, \(25\) cây.

Hướng dẫn giải

3.1. a) Ta có: \(C\left( x \right) = {x^4} + {x^3} - 4x - {x^4} + 3x + 7 + 3{x^2} - {x^2}\)

\(C\left( x \right) = \left( {{x^4} - {x^4}} \right) + {x^3} + \left( { - 4x + 3x} \right) + \left( {3{x^2} - {x^2}} \right) + 7\)

\(C\left( x \right) = {x^3} - x + 2{x^2} + 7\) hay \(C\left( x \right) = {x^3} + 2{x^2} - x + 7\).

b) Đa thức \(C\left( x \right)\) có hệ số cao nhất là \(1\); hệ số tự do là \(7\) và bậc là \(3\).

c) Ta có: \(C\left( 2 \right) = {2^3} - 2 + {2.2^2} + 7 = 21\).

\(C\left( 1 \right) = {1^3} - 1 + {2.1^2} + 7 = 9\)

\(C\left( { - 1} \right) = {\left( { - 1} \right)^3} - \left( { - 1} \right) + 2.{\left( { - 1} \right)^2} + 7 = 9\).

d) Ta có: \(D\left( x \right) - x + 2{x^2} - 1 = C\left( x \right)\) nên \(D\left( x \right) = C\left( x \right) + x - 2{x^2} + 1\)

Do đó, \(D\left( x \right) = {x^3} + 2{x^2} - x + 7 + x - 2{x^2} + 1 = {x^3} + 8\).

3.2. Ta có: \(G = {\left( {x - \frac{1}{2}} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 3} \right)^4} - 2025\)

Nhận thấy \({\left( {x - \frac{1}{2}} \right)^2} \ge 0\); \({\left( {y - 2} \right)^2} \ge 0\) và \({\left( {z + 3} \right)^4} \ge 0\).

Do đó, \({\left( {x - \frac{1}{2}} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 3} \right)^4} \ge 0\) nên \({\left( {x - \frac{1}{2}} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 3} \right)^4} - 2025 \ge - 2015\).

Dấu “=” xảy ra khi \({\left( {x - \frac{1}{2}} \right)^2} = 0;{\rm{ }}{\left( {y - 2} \right)^2} = 0;{\rm{ }}{\left( {z + 3} \right)^4} = 0\) hay \(x = \frac{1}{2};y = 2;z = 3\).

Vậy GTNN của \(G = - 2025\) khi \(x = \frac{1}{2};y = 2;z = 3\).

Hướng dẫn giải

4.1.

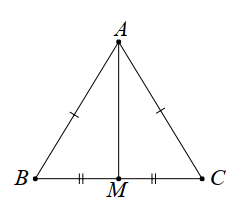
Xét

\(\Delta ABM\) và \(\Delta ACM\) có:

\(AB = AC\) (\(\Delta ABC\) cân tại \(A\))

\(\widehat B = \widehat C\)(\(\Delta ABC\) cân tại \(A\))

\(BM = MC\)

Suy ra \(\Delta ABM = \Delta ACM\) (c.g.c)

Do đó, \(\widehat {AMB} = \widehat {AMC}\) (hai góc tương ứng)

Mà hai góc \(\widehat {AMB} = \widehat {AMC}\) (hai góc tương ứng) (1)

Mà hai góc \(\widehat {AMB}\) và \(\widehat {AMC}\) là hai góc kề bù.

Suy ra \(\widehat {AMB} + \widehat {AMC} = 180^\circ \) (2)

Từ (1) và (2) suy ra \(\widehat {AMB} = \widehat {AMC} = \frac{{180^\circ }}{2} = 90^\circ \).

Do đó, \(AM \bot BC\) tại \(M.\)

Vậy \(AM\) là khoảng cách từ \(A\) đến cạnh \(BC\) của tam giác \(ABC.\)

4.2. Ta có \(BC > AB,BC > AC\) nên \(BC + BC + BC > AC + AB + BC\) tức là \(3BC > 18\) hay \(BC > 6.\)

Ta có \(BC < AC + AB\) nên \(BC + BC < AB + AC + BC\), tức là \(2BC < 18\) nên \(BC < 9\).

Từ đây suy ra \(6 < BC < 9\) và \(BC\) là một số tự nhiên chẵn nên \(BC = 8{\rm{ cm}}{\rm{.}}\)

Hướng dẫn giải

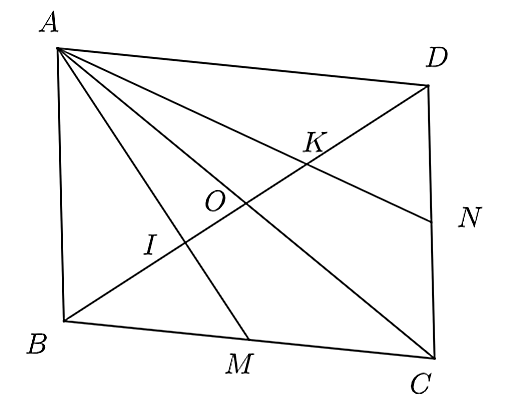
a) Xét \(\Delta ABC\), ta có: \(O\) là trung điểm của \(AC\), \(M\) là trung điểm của \(BC\).

Do đó, \(BO,AM\) là các đường trung tuyến của \(\Delta ABC\).

Mà \(BO\) cắt \(AM\) tại \(I\) nên \(I\) là trọng tâm của \(\Delta ABC\).

Xét \(\Delta ADC\), ta có: \(O\) là trung điểm của \(AC\), \(N\) là trung điểm của \(DC\).

Do đó, \(DO,AN\) là các đường trung tuyến của \(\Delta ADC\).

Mà \(DO\) cắt \(AN\) tại \(K\) nên \(K\) là trọng tâm của \(\Delta ADC\).

b) Xét \(\Delta ABC\) có \(I\) là trọng tâm nên \(IO = \frac{1}{3}BO\).

Xét \(\Delta ADC\) có \(K\) là trọng tâm nên \(KO = \frac{1}{3}DO\).

Mà \(O\) là trung điểm của \(BD\) nên \(BO = DO\).

Do đó, ta có: \(IO + KO = \frac{1}{3}BO + \frac{1}{3}DO = \frac{2}{3}BO\) hay \(IK = \frac{2}{3}BO\).

Do đó, \(BI = IK = KD = \frac{2}{3}BO = \frac{2}{3}DO.\)