(3,0 điểm)

3.1. Cho đa thức \(C\left( x \right) = {x^4} + {x^3} - 4x - {x^4} + 3x + 7 + 3{x^2} - {x^2}\).

a) Thu gọn và sắp xếp đa thức theo lũy thừa giảm dần của biến.

b) Chỉ ra hệ số cao nhất, hệ số tự do và bậc của đa thức \(C\left( x \right)\).

c) Tính các giá trị \(C\left( { - 2} \right),C\left( 1 \right),C\left( { - 1} \right).\)

d) Tìm đa thức \(D\left( x \right)\), biết \(D\left( x \right) - x + 2{x^2} - 1 = C\left( x \right)\).

3.2. Tính giá trị nhỏ nhất của đa thức \(G = {\left( {x - \frac{1}{2}} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 3} \right)^4} - 2025\).

Hướng dẫn giải

4.1.

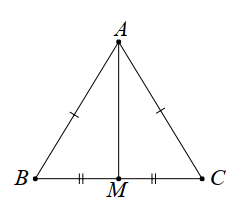
Xét

\(\Delta ABM\) và \(\Delta ACM\) có:

\(AB = AC\) (\(\Delta ABC\) cân tại \(A\))

\(\widehat B = \widehat C\)(\(\Delta ABC\) cân tại \(A\))

\(BM = MC\)

Suy ra \(\Delta ABM = \Delta ACM\) (c.g.c)

Do đó, \(\widehat {AMB} = \widehat {AMC}\) (hai góc tương ứng)

Mà hai góc \(\widehat {AMB} = \widehat {AMC}\) (hai góc tương ứng) (1)

Mà hai góc \(\widehat {AMB}\) và \(\widehat {AMC}\) là hai góc kề bù.

Suy ra \(\widehat {AMB} + \widehat {AMC} = 180^\circ \) (2)

Từ (1) và (2) suy ra \(\widehat {AMB} = \widehat {AMC} = \frac{{180^\circ }}{2} = 90^\circ \).

Do đó, \(AM \bot BC\) tại \(M.\)

Vậy \(AM\) là khoảng cách từ \(A\) đến cạnh \(BC\) của tam giác \(ABC.\)

4.2. Ta có \(BC > AB,BC > AC\) nên \(BC + BC + BC > AC + AB + BC\) tức là \(3BC > 18\) hay \(BC > 6.\)

Ta có \(BC < AC + AB\) nên \(BC + BC < AB + AC + BC\), tức là \(2BC < 18\) nên \(BC < 9\).

Từ đây suy ra \(6 < BC < 9\) và \(BC\) là một số tự nhiên chẵn nên \(BC = 8{\rm{ cm}}{\rm{.}}\)

Hướng dẫn giải

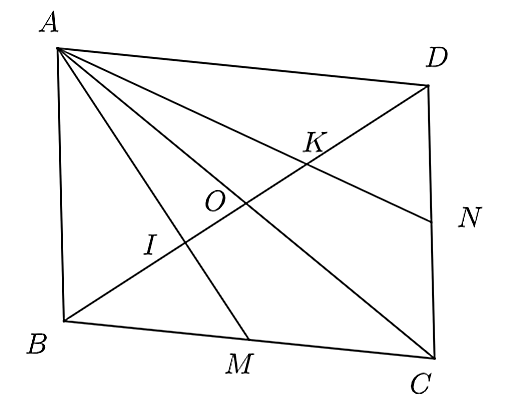
a) Xét \(\Delta ABC\), ta có: \(O\) là trung điểm của \(AC\), \(M\) là trung điểm của \(BC\).

Do đó, \(BO,AM\) là các đường trung tuyến của \(\Delta ABC\).

Mà \(BO\) cắt \(AM\) tại \(I\) nên \(I\) là trọng tâm của \(\Delta ABC\).

Xét \(\Delta ADC\), ta có: \(O\) là trung điểm của \(AC\), \(N\) là trung điểm của \(DC\).

Do đó, \(DO,AN\) là các đường trung tuyến của \(\Delta ADC\).

Mà \(DO\) cắt \(AN\) tại \(K\) nên \(K\) là trọng tâm của \(\Delta ADC\).

b) Xét \(\Delta ABC\) có \(I\) là trọng tâm nên \(IO = \frac{1}{3}BO\).

Xét \(\Delta ADC\) có \(K\) là trọng tâm nên \(KO = \frac{1}{3}DO\).

Mà \(O\) là trung điểm của \(BD\) nên \(BO = DO\).

Do đó, ta có: \(IO + KO = \frac{1}{3}BO + \frac{1}{3}DO = \frac{2}{3}BO\) hay \(IK = \frac{2}{3}BO\).

Do đó, \(BI = IK = KD = \frac{2}{3}BO = \frac{2}{3}DO.\)