Phần I: Trắc nghiệm nhiều phương án lựa chọn
Cho hàm số \[y = - {x^2} + 4x + 1\]. Khẳng định nào sau đây sai?
Phần I: Trắc nghiệm nhiều phương án lựa chọn
Cho hàm số \[y = - {x^2} + 4x + 1\]. Khẳng định nào sau đây sai?
A. Trên khoảng \[\left( { - \infty ;1} \right)\], hàm số đồng biến.
B. Hàm số nghịch biến trên khoảng \[\left( {2; + \infty } \right)\] và đồng biến trên khoảng \[\left( { - \infty ;2} \right)\].
C. Trên khoảng \[\left( {3; + \infty } \right)\], hàm số nghịch biến.
D. Hàm số nghịch biến trên khoảng \[\left( {4; + \infty } \right)\] và đồng biến trên khoảng \[\left( { - \infty ;4} \right)\].
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: D
Đỉnh của parabol có hoành độ: \[{x_I} = - \frac{b}{{2a}} = 2\].
Vì \(a = - 1 < 0\) nên hàm số đồng biến trên khoảng \[\left( { - \infty ;2} \right)\] và nghịch biến trên khoảng \[\left( {2; + \infty } \right)\].
Mà \[\left( { - \infty ;1} \right) \subset \left( { - \infty ;2} \right)\] và \[\left( {3; + \infty } \right) \subset \left( {2; + \infty } \right)\].
Vậy khẳng định D sai.
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \[x\] là giá bán thực tế của mỗi quả bưởi da xanh (\[x\]: đồng, \[35\,000 \le x \le 60\,000\]).
Tương ứng với giá bán là \[x\] thì số quả bán được là:
\[30 + \frac{{10}}{{1\,000}}\left( {60\,000 - x} \right) = - \frac{1}{{100}}x + 630\].
Gọi \[f\left( x \right)\] là hàm lợi nhuận thu được (\[f\left( x \right)\]: đồng), ta có:
Lợi nhuận thu được lớn nhất khi hàm \[f\left( x \right)\] đạt giá trị lớn nhất trên \[\left[ {35000\,;60000} \right]\].
Ta có:
\[ \Rightarrow \mathop {\max }\limits_{x \in \left[ {35\,000\,;60\,000} \right]} {\rm{ }}f\left( x \right) = f\left( {49\,000} \right) = 1\,960\,000\].
Vậy với giá bán \[49\] nghìn đồng mỗi quả bưởi thì cửa hàng thu được lợi nhuận lớn nhất.
Đáp án: 49.
Lời giải
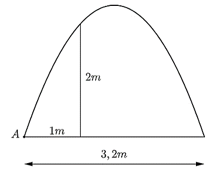
Chọn hệ trục tọa độ \(Oxy\) như hình vẽ.
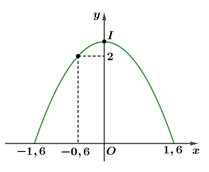
Khi đó đường parabol \(\left( P \right)\) có phương trình dạng \(y = a{x^2} + bx + c\) \(\left( {a \ne 0} \right)\) sẽ đi qua ba điểm có tọa độ là \(\left( { - 1,6;0} \right)\), \(\left( {1,6;0} \right)\) và \(\left( { - 0,6;2} \right)\).
Ta có hệ phương trìnhSuy ra phương trình đường parabol \(\left( P \right)\) là \(y = - \frac{{10}}{{11}}{x^2} + \frac{{128}}{{55}}\).
Giao điểm của \(\left( P \right)\) với trục \(Oy\) là đỉnh \(I\left( {0;\frac{{128}}{{55}}} \right)\).
Vậy chiều cao của cái cổng là \(OI = \frac{{128}}{{55}} \approx 2,33\,\,\left( {\rm{m}} \right)\).
Đáp án: \(2,33\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Hình \[1\].
B. Hình \[2\].
C. Hình \[3\].
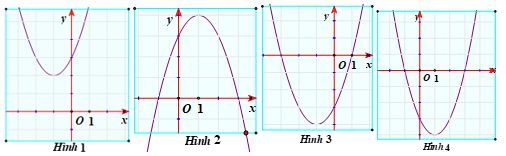
D. Hình \[4\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo