Mặt cắt ngang của một ống dẫn khí nóng là hình vành khuyên như Hình vẽ. Khí bên trong ống được duy trì ở 150 $°C$. Biết rằng nhiệt độ $T(°C)$ tại điềm \({\rm{A}}\) trên thành ống là hàm số của khoảng cách \(x(\;{\rm{cm}})\) từ \({\rm{A}}\) đến tâm của mặt cắt và \({T^\prime }(x) =  - \frac{{30}}{x}\quad (6 \le x \le 8).\)

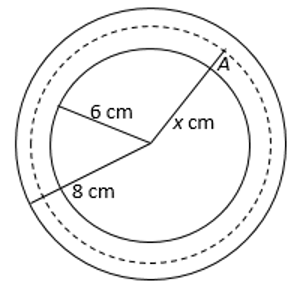
(Nguồn: Y.A.Çengel, A.I.Gahjar, Heat and Mass Transfer, Mc Graw Hill, 2015)

Tìm nhiệt độ mặt ngoài của ống.

Một ô tô đang di chuyển với tốc độ 20m/s thì hãm phanh nên tốc độ (m/s) của xe thay đổi theo thời gian t (giây) được tính theo công thức: \[v(t) = 20 - 5t,{\rm{ }}(0 \le t \le 4).\]

a) Kể từ lúc hãm phanh đến khi dừng, ô tô đi được quãng đường bao nhiêu?

b) Tính tốc độ trung bình của xe trong khoảng thời gian đó.

Giá trị trung bình của hàm số liên tục f(x) trên đoạn [a; b] được định nghĩa là \[\frac{1}{{b - a}}\int\limits_a^b {f(x)dx} \]. Giả sử nhiệt độ (tính bằng °C) tại thời điểm t giờ trong khoảng thời gian từ 6 giờ sáng đến 12 giờ trưa ở một địa phương vào một ngày nào đó được mô hình hoá bởi hàm số \[T\left( t \right) = 20 + 1,5\left( {t - 6} \right),{\rm{ }}6 \le t \le 12\].Tìm nhiệt độ trung bình vào ngày đó trong khoảng thời gian từ 6 giờ sáng đến 12 giờ trưa.

Ta biết rằng hàm cầu liên quan đến giá p của một sản phẩm với nhu cầu của người tiêu dùng, hàm cung liên quan đến giá p của sản phẩm với mức độ sẵn sàng cung cấp sản phẩm của nhà sản xuất. Điểm cắt nhau \(\left( {{{\rm{x}}_0};{{\rm{P}}_0}} \right)\) của đồ thị hàm cầu \({\rm{p}} = {\rm{D}}({\rm{x}})\) và đồ thị hàm cung p \( = {\rm{S}}({\rm{x}})\) được gọi là điểm cân bằng.

Các nhà kinh tế gọi diện tích của hình giới hạn bởi đồ thị hàm cầu, đường ngang \({\rm{p}} = {{\rm{p}}_0}\) và đường thẳng đứng \({\rm{x}} = 0\) là thặng dư tiêu dùng. Tương tự, diện tích của hình giới hạn bởi đồ thị của hàm cung, đường nằm ngang \({\rm{p}} = {{\rm{p}}_0}\) và đường thẳng đứng \(x = 0\) được gọi là thặng dư sản xuất, như trong Hình 4.19.

(Theo R.Larson, Brief Calculus: An Applied Approach, \({8^{{\rm{th }}}}\) edition, Cengage Learning, 2009).

Giả sử hàm cung và hàm cầu của một loại sản phẩm được mô hình hóa bởi:

Hàm cầu: \(p =  - 0,36x + 9\) và hàm cung: \(p = 0,14x + 2\), trong đó \(x\) là số đơn vị sản phẩm. Tìm thặng dư tiêu dùng và thặng dư sản xuất cho sản phẩm này.

Ở nhiệt độ 370C, một phản ứng hóa học từ chất A, chuển hóa thành sản phầm B theo phương trình phản ứng \[A \to B\]. Giả sử y(x) là nồng độ chất A ( đơn vị mol L-1) tại thời gian x (giây), y(x) > 0 với \[x \ge 0\], thỏa mãn hệ thức \[y'(x) =  - {7.10^{ - 4}}y(x)\] với mọi \[x \ge 0\]. Biết rằng tại x = 0, nồng độ (đầu) của A là 0,05 mol L-1.

a) Xét hàm số f(x) = lny(x) với \[x \ge 0\]. Hãy tính f’(x), từ đó hãy tìm hàm số f(x).

b) Giả sử ta tính nồng độ trung bình chất A (đơn vị mol L-1) từ thời điểm a (giây) đến thời điểm b (giây) với \[0 < a < b\] theo công thức \[\frac{1}{{b - a}}\int\limits_a^b {f(x)dx} \]. Xác định nồng độ trung bình của chất A từ thời điểm 15 giây đến thời điểm 30 giây.

Sau khi được thả rơi tự do từ độ cao 100 m, một vật rơi xuống với tốc độ v(t)=10t (m/s), trong đó t là thời gian tính theo giây kể từ khi thả vật.

a) Tính quãng đường s(t) vật di chuyển được sau thời gian t giây (trong khoảng thời gian vật đang rơi).

b) Sau bao nhiêu giây thì vật chạm đất? Tính tốc độ rơi trung bình của vật.

Một vật chuyển động dọc theo một đường thẳng sao cho vận tốc của nó tại thời điểm t (giây) là \[v(t) = {t^2} - t - 6\] (m/s).

a) Tìm độ dịch chuyển của vật trong khoảng thời gian \[1 \le t \le 4\], tức là tính \[\int\limits_1^4 {v(t)dt} \].

b) Tìm tổng quãng đường vật đi được trong khoảng thời gian này, tức là tính \[\int\limits_1^4 {\left| {v(t)} \right|dt} \].

Tại một nhà máy, gọi C(x) là tổng chi phí (tỉnh theo triệu đồng) để sản xuất x tấn sản phẩm A trong một tháng. Khi đó, đạo hàm C'(x), gọi là chi phi cận biên, cho biết tốc độ gia tăng tổng chi phí theo lượng gia tăng sản phẩm được sản xuất. Giả sử chi phí cận biên (tính theo triệu đồng trên tấn) của nhà máy được ước lượng bởi công thức: \[C'(x) = 5 - 0,06x + 0,00072{x^2}\] với \[0 \le x \le 150\]. Biết rằng C(0) = 30 triệu đồng, gọi là chi phí cố định. Tính tổng chi phí khi nhà máy sản xuất 100 tấn sản phẩm A trong tháng.