Một vật chuyển động được cho bởi đồ thị như hình bên.

a) Tính quãng đường mà vật di chuyển được trong 1 giây đầu tiên.
b) Tính quãng đường mà vật di chuyển được trong 2 giây đầu tiên.
Một vật chuyển động được cho bởi đồ thị như hình bên.

a) Tính quãng đường mà vật di chuyển được trong 1 giây đầu tiên.
b) Tính quãng đường mà vật di chuyển được trong 2 giây đầu tiên.
Quảng cáo
Trả lời:
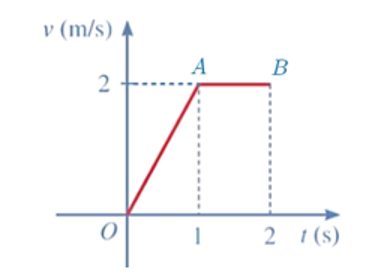
Gọi phương trình đường thẳng OA là \({\rm{v}}({\rm{t}}) = {\rm{at}}({\rm{a}} \ne 0)\).
Vi OA đi qua điểm \({\rm{A}}(1;2)\) nên với \({\rm{t}} = 1\) thì \({\rm{v}} = 2\), ta có \(2 = {\rm{a}} \cdot 1\), suy ra \({\rm{a}} = 2\).
Do đó, \({\rm{OA}}:{\rm{v}}({\rm{t}}) = 2{\rm{t}}\).
a) Trong 1 giây đầu tiên, vận tốc của vật được biểu diễn bởi hàm số \(v(t) = 2t\) \(({\rm{m}}/{\rm{s}})\).
Quãng đường mà vật di chuyển được trong 1 giây đầu tiên là:
\({s_1} = \int_0^1 2 tdt = \left. {{t^2}} \right|_0^1 = {1^2} - {0^2} = 1(\;{\rm{m}}).\)
b) Trong khoảng thời gian từ thời điểm \(t = 1\) (giây) đến thời điểm \(t = 2\) (giây), vận tốc của vật được biểu diễn bởi hàm số hằng \(v({\rm{t}}) = 2\).
Quãng đường mà vật di chuyển được trong khoảng thời gian từ thời điểm \({\rm{t}} = 1\) (giây) đến thời điểm \(t = 2\) (giây) là:
\({s_2} = \int_1^2 2 dt = \left. {2t} \right|_1^2 = 2(2 - 1) = 2(\;{\rm{m}}).\)
Vậy quãng đường mà vật di chuyển được trong 2 giây đầu tiên là \(s = 1 + 2\) = 3 (m).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Ta có \({\rm{f}}({\rm{x}}) = \ln {\rm{y}}({\rm{x}})\). Lấy đạo hàm hai vế ta được: \({{\rm{f}}^\prime }({\rm{x}}) = \frac{{{y^\prime }(x)}}{{y(x)}}\).
Mà \({y^\prime }({\rm{x}}) = - 7 \cdot {10^{ - 4}}y(x)\), suy ra \( = - 7 \cdot {10^{ - 4}}\).
Do đó, \({f^\prime }(x) = - 7 \cdot {10^{ - 4}}\).
Hàm số \(f(x)\) là một nguyên hàm của hàm số \({f^\prime }(x)\).
Ta có \(\int {{f^\prime }} (x)dx = \int {\left( { - 7 \cdot {{10}^{ - 4}}} \right)} dx = - 7 \cdot {10^{ - 4}}x + C\).
Suy ra \(f(x) = - 7 \cdot {10^{ - 4}}x + C\).
Mà \(f(x) = \ln y(x)\) nên \(\ln y(x) = - 7 \cdot {10^{ - 4}}x + C\). Suy ra \(y(x) = {e^{ - 7 \cdot {{10}^{ - 4}}x + C}}\).
Vì tại \(x = 0\), nồng độ ban đầu của chất \(A\) là \(0,05\;{\rm{mo}}{{\rm{l}}^{ - 1}}\), tức là \({\rm{y}}(0) = 0,05\) nên \({e^C} = 0,05 \Leftrightarrow C = \ln 0,05\).
Vậy \(f(x) = - 7 \cdot {10^{ - 4}}x + \ln 0,05\).
b) Từ câu a, ta có \(y(x) = {e^{ - 7 \cdot {{10}^{ - 4}}x + \ln 0,05}}\).
Khi đó nồng độ trung bình của chất A từ thời điểm 15 giây đến thời điểm 30 giây là:
\(\begin{array}{l}\frac{1}{{30 - 15}}\int_{15}^{30} y (x)dx = \frac{1}{{15}}\int_{15}^{30} {{e^{ - 7 \cdot {{10}^{ - 4}}x + \ln 0,05}}} dx = \frac{{{e^{\ln 0,05}}}}{{15}}\int_{15}^{30} {{{\left( {{e^{ - 7 \cdot {{10}^{ - 4}}}}} \right)}^x}} dx\\ = \left. {\frac{1}{{300}} \cdot \frac{{{{\left( {{e^{ - 7 \cdot {{10}^4}}}} \right)}^x}}}{{\ln {e^{ - 7 \cdot {{10}^{ - 4}}}}}}} \right|_{15}^{30} = \frac{{ - 100}}{{21}}\left( {{e^{ - 7 \cdot {{10}^{ - 4}} \cdot 30}} - {e^{ - 7 \cdot {{10}^{ - 4}} \cdot 15}}} \right) \approx 0,049\left( {\;{\rm{mol}}\;{{\rm{L}}^{ - 1}}} \right).\end{array}\)
Lời giải
Giả sử vật chuyển động trên một trục nằm ngang, chiểu dương hướng từ trái sang phải.
a) Ta có \(\int_1^4 v (t){\rm{d}}t = \int_1^4 {\left( {{t^2} - t - 6} \right)} {\rm{d}}t = \left. {\left( {\frac{1}{3}{t^3} - \frac{1}{2}{t^2} - 6t} \right)} \right|_1^4 = - \frac{9}{2}\).
Vậy trong khoảng thời gian \(1 \le t \le 4\), vật dịch chuyển sang bên trái được \(4,5\;{\rm{m}}\) so với vị trí tại thời điểm \(t = 1\) (giây) (Trong quá trình chuyển động, lúc thì vật đi sang trái, lúc thì đi sang phải, nhưng tại thời điểm \(t = 4\) (giây) thì vật có vị trí nằm ở phía bên trái và cách vị trí của vật tại thời điểm \(t = 1\) (giây) một khoảng là \(4,5\;{\rm{m}}\) ).
b) Ta có
\[\begin{array}{l}\int_1^4 | v(t)|{\rm{d}}t = \int_1^4 {\left| {{t^2} - t - 6} \right|} {\rm{d}}t = \int_1^3 {\left| {{t^2} - t - 6} \right|} {\rm{d}}t + \int_3^4 {\left| {{t^2} - t - 6} \right|} {\rm{d}}t = \int_1^3 {\left( { - {t^2} + t + 6} \right)} {\rm{d}}t + \int_3^4 {\left( {{t^2} - t - 6} \right)} {\rm{d}}t\\ = \left. {\left( {\frac{{ - 1}}{3}{t^3} + \frac{1}{2}{t^2} + 6t} \right)} \right|_1^3 + \left. {\left( {\frac{1}{3}{t^3} - \frac{1}{2}{t^2} - 6t} \right)} \right|_3^4 = \frac{{22}}{3} + \frac{{17}}{6} = \frac{{61}}{6}.\end{array}\]
Vậy tổng quãng đường vật đi được trong khoảng thời gian \(1 \le t \le 4\) (giây) (tính cả quãng đường lúc đi sang trái, quãng đường lúc đi sang phải) là \(\frac{{61}}{6}\;{\rm{m}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.