Một vật chuyển động trong 4 giờ với vận tốc \(v\left( {km/h} \right)\) phụ thuộc thời gian \(t\left( h \right)\) có đồ thị của vận tốc. Trong khoảng thời gian 3 giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một phần của đường Parabol có đỉnh \(I\left( {2;9} \right)\) với trục đối xứng song song với trục tung, khoảng thời gian còn lại đồ thị là một đoạn thẳng song song với trục hoành . Tính quãng đuờng \(s\) mà vật chuyển động trong 4 giờ đó.

          Hai ô tô xuất phát tại cùng một thời điểm trên cùng đoạn thẳng \(AB\), ô tô thứ nhất bắt đầu xuất phát từ \(A\) và đi theo hướng từ \(A\) đến \(B\) với vận tốc \({v_s}\left( t \right) = 2t + 1\,\left( {km/h} \right)\); ô tô thứ hai xuất phát từ \(O\) cách \(A\) một khoảng \(22\,km\) và đi theo hướng từ \(A\) đến \(B\) với vận tốc \(10\,km/h\), sau một khoảng thời gian người lái đạp phanh; từ thời điểm đó, ô tô thứ hai chuyển động chậm dần đều với vận tốc \({v_s}\left( t \right) =  - 5t + 20\,\left( {km/h} \right)\). Hỏi sau khoảng thời gian bao lâu kể từ khi xuất phát hai ô tô đó gặp nhau?

    Một chất điểm \(A\) xuất phát từ \(O\), chuyển động thẳng với vận tốc biến thiên theo thời gian bởi quy luật \(v\left( t \right) = \frac{1}{{100}}{t^2} + \frac{{13}}{{30}}t \left( {{\rm{m/s}}} \right)\), trong đó \(t\) (giây) là khoảng thời gian tính từ lúc \(A\) bắt đầu chuyển động. Từ trạng thái nghỉ, một chất điểm \(B\) cũng xuất phát từ \(O\), chuyển động thẳng cùng hướng với \(A\) nhưng chậm hơn \(10\) giây so với \(A\) và có gia tốc bằng \(a \left( {{\rm{m/}}{{\rm{s}}^2}} \right)\) (\(a\) là hằng số). Sau khi \(B\) xuất phát được \(15\) giây thì đuổi kịp \(A\). Vận tốc của \(B\) tại thời điểm đuổi kịp \(A\) bằng

Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc \({v_1}\left( t \right) = 7t\left( {m/s} \right)\). Đi được \(5\left( s \right)\), người lái xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc là \(a =  - 70\left( {m/{s^2}} \right)\). Tính quãng đường \(S\) từ lúc ô tô bắt đầu chuyển bánh cho đến khi dừng hẳn.

     Một ô tô chạy với vận tốc \({v_0}\left( {{\rm{m/s}}} \right)\)thì gặp chướng ngại vật nên người lái xe đạp phanh. Từ thời điểm đó ôtô chuyển động chậm dần với gia tốc \(a =  - 8t\left( {{\rm{m/}}{{\rm{s}}^{\rm{2}}}} \right)\)trong đó \(t\)là thời gian tính bằng giây. Biết từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển được \(12{\rm{m}}\). Tính \({v_0}?\)

         Một vật chuyển động thẳng có đồ thị vận tốc theo thời gian trong 6 giờ đầu tiên như hình vẽ bên dưới. Biết rằng đoạn đồ thị \(ABC\) là một đường parabol và \(B\) là đỉnh của parabol. Quãng đường vật đi được trong 3 giờ đầu tiên là

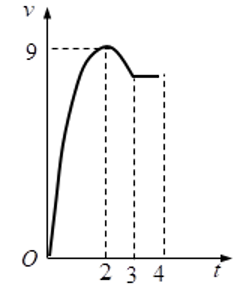
        Một vật chuyển động trong 3 giờ với vận tốc \(v(km/h)\) phụ thuộc vào thời gian \(t(h)\) có đồ thị vận tốc như hình bên. Trong thời gian 1 giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một phần của đường parabol có đỉnh \(I(2;9)\) và trục đối xứng song song với trục tung, khoảng thời gian còn lại đồ thị là một đoạn thẳng song song với trục hoành. Tính quãng đường \(s\) mà vật chuyển động được trong 3 giờ đó (kết quả làm tròn đến hàng phần trăm)