Câu hỏi:
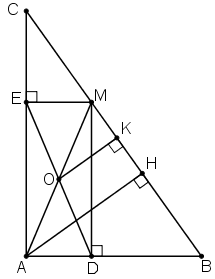
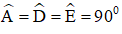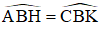12/07/2024 22,579Cho tam giác ABC vuông tại A. Lấy M là một điểm bất kì thuộc cạnh BC. Gọi MD là đường vuông góc kẻ từ M đến AB, ME là đường vuông góc kẻ từ M đến AC, O là trung điểm của DE.
a) Chứng minh rằng ba điểm A, O, M thẳng hàng.
b) Khi điểm M di chuyển trên cạnh BC thì điểm O di chuyển trên đường nào?
c) Điểm M ở vị trí nào trên cạnh BC thì AM có độ dài nhỏ nhất?
Câu hỏi trong đề: Giải toán 8: Chương 1: Tứ giác !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Tứ giác ADME có: 
⇒ ADME là hình chữ nhật
O là trung điiểm của đường chéo DE nên O cũng là trung điểm của đường chéo AM.
Vậy A, O, M thẳng hàng.
b) Kẻ AH ⊥ BC; OK ⊥ BC.
Ta có OA = OM, OK // AH (cùng vuông góc BC)
⇒ MK = KH
⇒ OK là đường trung bình của ΔMAH
⇒ OK = AH/2.
⇒ điểm O cách BC một khoảng cố định bằng AH/2
⇒ O nằm trên đường thẳng song song với BC.
Mặt khác khi M trùng C thì O chính là trung điểm của AC, khi M trùng B thì O chính là trung điểm của AB.
Vậy O di chuyển trên đoạn thẳng PQ là đường trung bình của tam giác ABC.
c) Vì AH là đường cao hạ từ A đến BC nên AM ≥ AH (trong tam giác vuông thì cạnh huyền là cạnh lớn nhất).
Vậy AM nhỏ nhất khi M trùng H.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
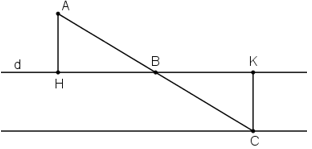
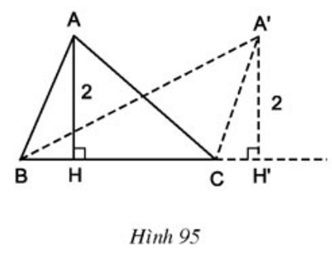
Gọi H, K là hình chiếu của A và C trên đường thẳng d.
⇒ Khoảng cách từ A đến d bằng AH
⇒ AH = 2cm.
Xét ΔAHB vuông tại H và ΔCKB vuông tại K có:
AB = BC
⇒ ΔAHB = ΔCKB (cạnh huyền – góc nhọn)
⇒ CK = AH = 2cm.
Vậy điểm C nằm trên đường thẳng song song với d, không đi qua A và cách d 2cm.
Lời giải
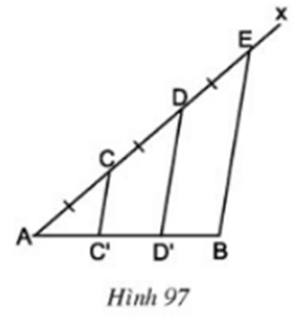
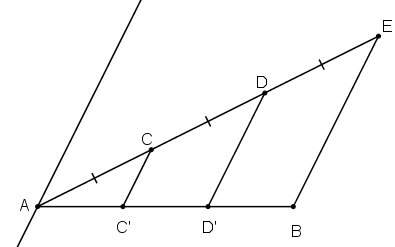
Kẻ đường thẳng At // CC’ // DD’ // BE như hình vẽ.
Ta có: AC = CD = DE
⇒ At, CC’, DD‘, BE là các đường thẳng song song cách đều
⇒ AC’ = C’D’ = D’B
hay đoạn thẳng AB bị chia ra làm 3 phần bằng nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 25
-
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
-
Đề cuối kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án- Đề 4
-
Bộ 10 đề thi giữa kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án (Đề 5)
-
Dạng 8: Bài luyện tập 3 dạng 4. Tổng hợp có đáp án