Bài tập: Đường trung bình Của tam giác, của hình thang
39 người thi tuần này 3.5 3 K lượt thi 10 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 06
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 05
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 04
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 03
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 02
Bộ 10 đề thi cuối kì 2 Toán 8 Cánh diều có đáp án - Đề 01
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức có đáp án - Đề 10
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức có đáp án - Đề 9
Danh sách câu hỏi:
Lời giải
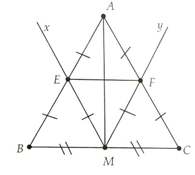
a) Mx đi qua trung điểm M của BC và song song với AC. Suy ra Mx đi qua trung điểm E của AB (theo Định lí 1).
Tương tự, ta được F cũng là trung điểm của AC. Khi đó EF trở thành đường trung bình của tam giác ABC;
b) Do ME và MF cũng là đường trung bình nên có ME = MF = AE = AF. Suy ra AM là đường trung trực của EF.
Lời giải
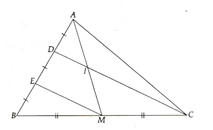
a) Ta có EM là đường trung bình của tam giác BCD Þ ĐPCM.
b) DC đi qua trung điểm D của AE và song song với EM Þ DC đi qua trung điểm I của AM.
c) Vì DI là đường trung bình của tam giác AEM nên DI = (1/2) EM.(1)
Tương tự, ta được: EM = (1/2)DC (2)
Từ (1) và (2) Þ DC = 4DI
Lời giải
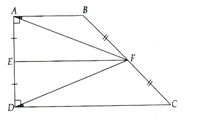
a) Ta có È là đường trung bình của hình thang ABCD.
Þ EF//AB.
Suy ra EF ^ AD
Khi đó EF vừa trung tuyến, vừa là đường cao của tam giác AFD Þ ĐPCM.
b) Tam giác AFD cân tại F nên
Suy ra
Lời giải
a) Gọi M và N lần lượt là giao điểm của AE, BF với CD.
Ta có: ngoài, ngoài.
Mà ngoài + ngoài = 1800 (do AB//CD)
, tức là tam giác ADE vuông tại E.
Khi đó, tam giác ADM cân tại D (do có DE vừa là đường phân giác, vừa là đường cao) và E là trung điểm của AM.
Chứng minh tương tự, ta được F olaf trung điểm của BN.
Từ khó, suy ra EF là đường trung bình của hình thang ABNM và ta được ĐPCM
b) Từ ý a),
Lưu ý: Có thể sử dụng tính chất đường phân giác để chứng minh
Lời giải
a) Ta có MN là đường trung bình của tam giác ABD
=> MN//AB
Tương tự, ta được MP//CD và MQ//AB, CD.
Như vậy, MN, MP, MQ cùng song song AB Þ ĐPCM.
b) Ta có:
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.