Cho tam giác ABC vuông tại A, kẻ đường cao AH. Từ H kẻ tia Hx vuông góc với AB tại P và tia Hy vuông góc vói AC tại Q. Trên các tia Hx, Hy lần lượt lấy các điếm D và E sao cho PH = PD, QH = QE. Chứng minh:
a) A là trung điểm của DE;
b) PQ =
c) PQ = AH
Câu hỏi trong đề: Bài tập: Đường trung bình Của tam giác, của hình thang !!
Quảng cáo
Trả lời:
a) Chứng minh được tam giác ADH và AEH cân tại A.
Khi đó: và AD = AH = AE.
Từ đó, suy ra được A, A, E thẳng hàng và A là trung điểm DE.
b) PQ là đường trung bình của tam giác DHE Þ ĐPCM.
c) Có AH = AD = AE = 0.5.DE, mà PQ = 0.5.DE Þ AH = PQ.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
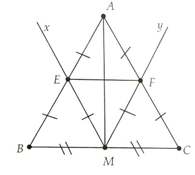
a) Mx đi qua trung điểm M của BC và song song với AC. Suy ra Mx đi qua trung điểm E của AB (theo Định lí 1).
Tương tự, ta được F cũng là trung điểm của AC. Khi đó EF trở thành đường trung bình của tam giác ABC;
b) Do ME và MF cũng là đường trung bình nên có ME = MF = AE = AF. Suy ra AM là đường trung trực của EF.
Lời giải
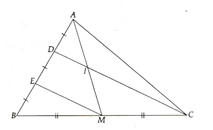
a) Ta có EM là đường trung bình của tam giác BCD Þ ĐPCM.
b) DC đi qua trung điểm D của AE và song song với EM Þ DC đi qua trung điểm I của AM.
c) Vì DI là đường trung bình của tam giác AEM nên DI = (1/2) EM.(1)
Tương tự, ta được: EM = (1/2)DC (2)
Từ (1) và (2) Þ DC = 4DI
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.