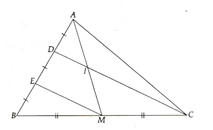
Cho tam giác ABC có AM là trung tuyến ứng vói BC. Trên cạnh AC lấy điểm D sao cho AD = (1/2) C. Kẻ Mx song song với BD và cắt AC tại E. Đoạn BD cắt AM tại I. Chứng minh:
a) AD = DE = EC;
b) SAIB = SIBM;
c)SABC = 2SIBC.
Câu hỏi trong đề: Bài tập: Đường trung bình Của tam giác, của hình thang !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Theo định lý 1, trong tam giác BDC có: M là trung điểm của BC, ME//BD Þ E là trung điểm của DC Þ DE = EC = 0.5.DC.
Suy ra AD = DE = EC.
b) Từ ý a) D là trung điểm của AE. Suy ra ID là đường trung bình của tam giác AME hay IA = IM.
Vậy SAIB= SIBM.
c) Hạ hai đường cao AH và IK của tam giác ABC và IBC
Chứng minh được IK là đường trung bình của tam giác AHM Þ IK = 0.5. AH.
Xét hai tam giác ABC và IBC có chung đáy BC và hai đường cao AH = 2IK Þ ĐPCM.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
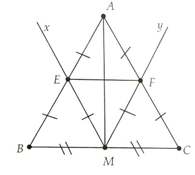
a) Mx đi qua trung điểm M của BC và song song với AC. Suy ra Mx đi qua trung điểm E của AB (theo Định lí 1).
Tương tự, ta được F cũng là trung điểm của AC. Khi đó EF trở thành đường trung bình của tam giác ABC;
b) Do ME và MF cũng là đường trung bình nên có ME = MF = AE = AF. Suy ra AM là đường trung trực của EF.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Ta có EM là đường trung bình của tam giác BCD Þ ĐPCM.
b) DC đi qua trung điểm D của AE và song song với EM Þ DC đi qua trung điểm I của AM.
c) Vì DI là đường trung bình của tam giác AEM nên DI = (1/2) EM.(1)
Tương tự, ta được: EM = (1/2)DC (2)
Từ (1) và (2) Þ DC = 4DI
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập