Thống kê tổng số giờ nắng trong tháng 9 tại một trạm quan trắc đặt ở Cà Mau trong các năm từ 2002 đến 2021 được thống kê như sau:

           111,6   134,9   130,3   134,2   140,9   109,3   154,4   156,3   116,1   96,7

           105,2   80,8     80,8     110      109      139      145      161      126      114

(Nguồn: Tổng cục Thống kê)

a) Hãy tính phương sai và độ lệch chuẩn của mẫu số liệu trên.

b) Hãy lập bảng tần số ghép nhóm với nhóm đầu tiên là [80; 98) và độ dài mỗi nhóm bằng 18. Tính phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm.

c) Hãy tính sai số tương đối của độ lệch chuẩn của mẫu số liệu ghép nhóm so với độ lệch chuẩn của mẫu số liệu gốc. (Kết quả các phép tính làm tròn đến hàng phần nghìn.)

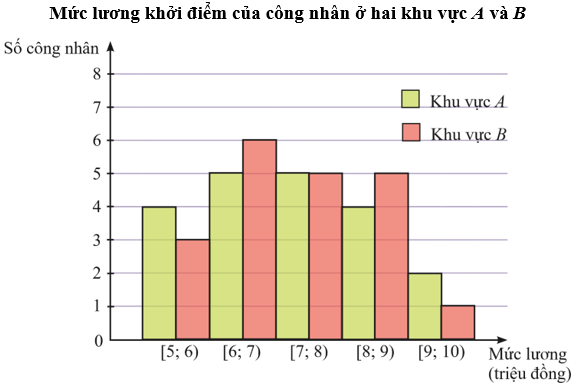
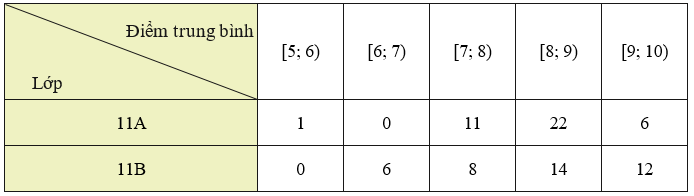
a) Từ Bảng 24, ta có các bảng thống kê sau:

b)

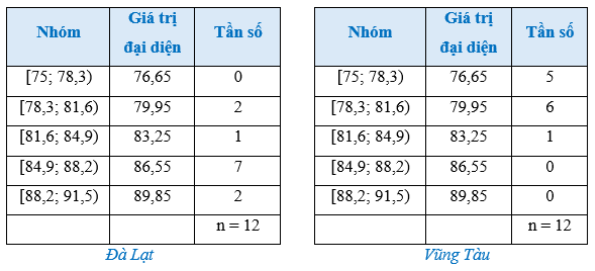
Đà Lạt

Khoảng biến thiên của mẫu số liệu ghép nhóm của Đà Lạt là: \({\rm{R}} = 91,5 - 78,3 = 13,2(\% ){\rm{. }}\)

Từ bảng thống kê trên, ta có bảng thống kê của mẫu số liệu ghép nhóm của Đà Lạt:

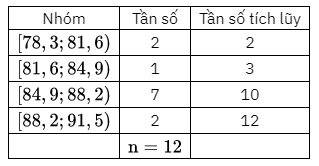
Số phần tử của mẫu là \({\rm{n}} = 12\).

Ta có: \(\frac{n}{4} = \frac{{12}}{4} = 3\) mà \(2 < 3\). Suy ra nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 3 . Xét nhóm 2 là nhóm \([81,6;84,9)\) có \(s = 81,6;h = 3,3;{n_2} = 1\) và nhóm 1 là nhóm \([78,3;81,6)\) có cf \(_1 = 2\).

Áp dụng công thức, ta có tứ phân vị thứ nhất là: \({Q_1} = 81,6 + \left( {\frac{{3 - 2}}{1}} \right) \cdot 3,3 = 84,9(\% ){\rm{. }}\)

Ta có: \(\frac{{3n}}{4} = \frac{{3 \cdot 12}}{4} = 9\) mà \(3 < 9 < 10\). Suy ra nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bẳng 9 . Xét nhóm 3 là nhóm \([84,9;88,2)\) có \(t = 84,9;1 = 3,3;{n_3} = 7\) và nhóm 2 là nhóm \([81,6;84,9)\) có cf \(_2 = 3\).

Áp dụng công thức, ta có tứ phân vị thứ ba là: \({Q_3} = 84,9 + \left( {\frac{{9 - 3}}{7}} \right) \cdot 3,3 \approx 87,7(\% )\)

Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm của Đà Lạt là: \({\Delta _Q} = {{\rm{Q}}_3} - {{\rm{Q}}_1} = 87,7 - 84,9 = 2,8(\% )\)

Số trung bình cộng của mẫu số liệu ghép nhóm của Đà Lạt là:

\(\bar x = \frac{{2 \cdot 79,95 + 1 \cdot 83,25 + 7 \cdot 86,55 + 2 \cdot 89,85}}{{12}} = \frac{{1028,7}}{{12}} = 85,725(\% ){\rm{. }}\)

Vậy phương sai của của mẫu số liệu ghép nhóm của Đà Lạt là:

\(\begin{array}{l}{s^2} = \frac{1}{{12}}.\left[ {2 \cdot {{(79,95 - 85,725)}^2} + 1 \cdot {{(83,25 - 85,725)}^2} + 7 \cdot {{(86,55 - 85,725)}^2} + 2 \cdot {{(89,85 - 85,725)}^2}} \right]\\{\rm{   }} = \frac{{111,6225}}{{12}} \approx 9,3\end{array}\)

Độ lệch chuẩn của mẫu số liệu ghép nhóm của Đà Lạt là: \(s \approx \sqrt {9,3}  \approx 3,05(\% )\).

Vũng Tàu

Khoảng biến thiên của mẫu số liệu ghép nhóm của Vũng Tàu là: \({{\rm{R}}^\prime } = 84,9 - 75 = 9,9(\% ){\rm{. }}\)

Từ bảng thống kê trên, ta có bảng thống kê của mẫu số liệu ghép nhóm của Vūng Tàu:

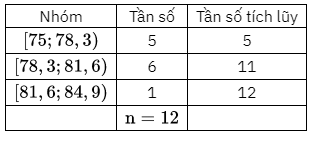
Số phần tử của mẫu là \({\rm{n}} = 12\).

Ta có: \(\frac{n}{4} = \frac{{12}}{4} = 3\) mà \(5 > 3\). Suy ra nhóm 1 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 3. Xét nhóm 1 là nhóm \([75;78,3)\) có \(s = 75;h = 3,3;{n_1} = 5\).

Áp dụng công thức, ta có tứ phân vị thứ nhất là:

\({Q_1} = 75 + \frac{3}{5} \cdot 3,3 = 76,98(\% )\)

Ta có: \(\frac{{3n}}{4} = \frac{{3 \cdot 12}}{4} = 9\) mà \(5 < 9 < 11\). Suy ra nhóm 2 là nhóm đầu tiền có tần số tích lūy lớn hơn hoặc bẳng 9 . Xét nhóm 2 là nhóm \([78,3;81,6)\) có \(t = 78,3;1 = 3,3;{n_2} = 6\) và nhóm 1 là nhóm \(\left[ {75;78,3} \right.\) ) có \({\rm{c}}{{\rm{f}}_1} = 5\).

Áp dụng công thức, ta có tứ phân vị thứ ba là: \(Q_3^\prime  = 78,3 + \left( {\frac{{9 - 5}}{6}} \right) \cdot 3,3 = 80,5(\% ).\)

Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm của Vũng Tàu là:

\(\Delta _{\rm{Q}}^\prime  = {\rm{Q}}_3^\prime  - {\rm{Q}}_1^\prime  = 80,5 - 76,98 = 3,52(\% ){\rm{. }}\)

Số trung bình cộng của mẫu số liệu ghép nhóm của Vũng Tàu là:

\(\overline {{x^\prime }}  = \frac{{5 \cdot 76,65 + 6 \cdot 79,95 + 1 \cdot 83,25}}{{12}} = \frac{{946,2}}{{12}} = 78,85(\% ).\)

Vậy phương sai của của mẫu số liệu ghép nhóm của Vũng Tàu là:

\({s'^2} = \frac{1}{{12}} \cdot \left[ {5 \cdot {{(76,65 - 78,85)}^2} + 6 \cdot {{(79,95 - 78,85)}^2} + 1 \cdot {{(83,25 - 78,85)}^2}} \right] = \frac{{50,82}}{{12}} = 4,235\)

Độ lệch chuẩn của mẫu số liệu ghép nhóm của Vūng Tàu là: \({s^\prime } = \sqrt {4,235}  \approx 2,06\) (\%).

c) Vì s' \( \approx 2,06 < {\rm{s}} \approx 3,05\) nên thành phố Vūng Tàu có độ ẩm không khí trung bình tháng đồng đều hơn thành phố Đà Lạt.