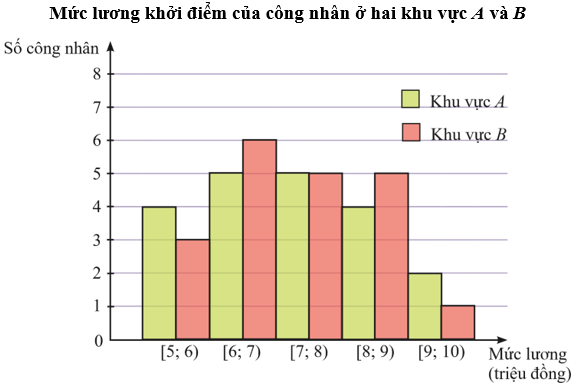
Thầy Tuấn thống kê lại điểm trung bình cuối năm của các học sinh lớp 11A và 11B ở bảng sau:
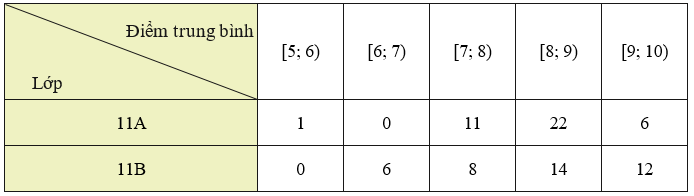
a) Nếu so sánh theo khoảng biến thiên thì học sinh lớp nào có điểm trung bình ít phân tán hơn?
b) Nếu so sánh theo độ lệch chuẩn thì học sinh lớp nào có điểm trung bình ít phân tán hơn?
Thầy Tuấn thống kê lại điểm trung bình cuối năm của các học sinh lớp 11A và 11B ở bảng sau:
a) Nếu so sánh theo khoảng biến thiên thì học sinh lớp nào có điểm trung bình ít phân tán hơn?
b) Nếu so sánh theo độ lệch chuẩn thì học sinh lớp nào có điểm trung bình ít phân tán hơn?
Quảng cáo
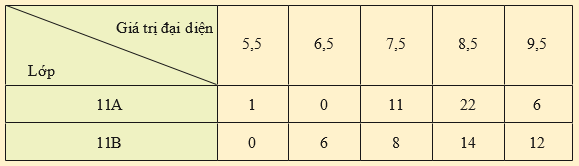
Trả lời:
Giải bởi Vietjack
a) Khoảng biến thiên của điểm số học sinh lớp 11A là: 10 – 5 = 5.
Khoảng biến thiên của điểm số học sinh lớp 11B là: 10 – 6 = 4.
Nếu so sánh theo khoảng biến thiên thì điểm trung bình của các học sinh lớp 11B ít phân tán hơn điểm trung bình của các học sinh lớp 11A.
b) Ta có bảng thống kê điểm trung bình theo giá trị đại diện
• Xét mẫu số liệu của lớp 11A: Cỡ mẫu là n1 = 1 + 11 + 22 + 6 = 40.
Số trung bình của mẫu số liệu ghép nhóm là: \[{\bar x_1} = \frac{{1.5,5 + 11.7,5 + 22.8,5 + 6.9,5}}{{40}} = 8,3\]
Phương sai của mẫu số liệu ghép nhóm: S12 = \[\frac{1}{{40}}\] (1 . 5,52 + 11 . 7,52 + 22 . 8,52 + 6 . 9,52) – 8,32 = 0,61.
Độ lệch chuẩn của mẫu số liệu ghép nhóm là \[{S_1} \approx \sqrt {0,61} \]
• Xét mẫu số liệu của lớp 11B: Cỡ mẫu là n2 = 6 + 8 + 14 + 12 = 40.
Số trung bình của mẫu số liệu ghép nhóm là \[{\bar x_2} = \frac{{6.6,5 + 8.7,5 + 14.8,5 + 12.9,5}}{{40}} = 8,3\]
Phương sai của mẫu số liệu ghép nhóm: S22 = \[\frac{1}{{40}}\] (6. 6,52 + 8 . 7,52 + 14 . 8,52 + 12 . 9,52) – 8,32 = 1,06.
Độ lệch chuẩn của mẫu số liệu ghép nhóm là \[{S_2} \approx \sqrt {1,06} \]
Do S1 < S2 nên nếu so sánh theo độ lệch chuẩn thì học sinh lớp 11A có điểm trung bình ít phân tán hơn học sinh lớp 11B.
Chú ý: Trong ví dụ trên, kết quả so sánh độ phân tán theo giá trị trung bình và độ lệch chuẩn có sự khác biệt. Điều này là do mẫu số liệu của học sinh lớp 11A có một giá trị ngoại lệ.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có bảng thống kê giá đóng cửa theo giá trị đại diện:
Xét mẫu số liệu của cổ phiếu A:
Số trung bình của mẫu số liệu ghép nhóm là \[{\bar x_1} = \frac{{8.121 + 9.123 + 12.125 + 10.127 + 11.129}}{{50}} = 125,28\]
Phương sai của mẫu số liệu ghép nhóm là
\[S_1^2\] = \[\frac{1}{{50}}\] (8 . 1212 + 9 . 1232 + 12 . 1252 + 10 . 1272 + 11 . 1292) – (125,28)2 = 7,5216.
Độ lệch chuẩn của mẫu số liệu ghép nhóm là \[{S_1} = \sqrt {S_1^2} = \sqrt {7,5216} \]
Xét mẫu số liệu của cổ phiếu B:
Số trung bình của mẫu số liệu ghép nhóm là \[{\bar x_2} = \frac{{16.121 + 4.123 + 3.125 + 6.127 + 21.129}}{{50}} = 125,28\]
Phương sai của mẫu số liệu ghép nhóm là
\[S_2^2\]=\[\frac{1}{{50}}\] (16 . 1212 + 4 . 1232 + 3 . 1252 + 6 . 1272 + 21 . 1292) – (125,48)2 = 12,4096.
Độ lệch chuẩn của mẫu số liệu ghép nhóm là \[{S_2} = \sqrt {S_2^2} = \sqrt {12,4096} \]
Vậy nếu đánh giá độ rủi ro theo phương sai và độ lệch chuẩn thì cổ phiếu A có độ rủi ro thấp hơn cổ phiếu B.
Lời giải
a) Cỡ mẫu là n = 20.
Số trung bình của mẫu số liệu trên là: \[{\bar x_1} = \frac{{111,6 + 134,9 + ... + 114}}{{20}} = 122,755\]
Phương sai của mẫu số liệu trên là: S12 =\[\frac{1}{{20}}\] (111,62 + 134,92 + … + 1142) – 122,7552 ≈ 515,453.
Độ lệch chuẩn của mẫu số liệu trên là \[{S_1} \approx \sqrt {515,453} \approx 22,704\]
b) Ta có bảng sau:
Số trung bình của mẫu số liệu ghép nhóm là: \[{\bar x_2} = \frac{{3.89 + 6.107 + 3.125 + 5.143 + 3.161}}{{20}} = 124,1\]
Phương sai của mẫu số liệu ghép nhóm là
S22 = \[\frac{1}{{20}}\] (3 . 892 + 6 . 1072 + 3 . 1252 + 5 . 1432 + 3 . 1612) – 124,12 = 566,19.
Độ lệch chuẩn của mẫu số liệu ghép nhóm là \[{S_2} \approx \sqrt {566,19} \approx 23,795\]
c) Sai số tương đối của độ lệch chuẩn của mẫu số liệu ghép nhóm so với độ lệch chuẩn của mẫu số liệu gốc là
\[\frac{{\left| {{S_2} - {S_1}} \right|}}{{{S_1}}} = \frac{{\left| {23,795 - 22,704} \right|}}{{22,704}} \cdot 100\% \approx 4,805\% \]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập