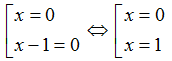Câu hỏi:
13/07/2024 3,624Trong các giá trị t = -1, t = 0 và t = 1, giá trị nào là nghiệm của phương trình: (t + 2)2 = 3t + 4?
Câu hỏi trong đề: Giải toán 8: Chương 3: Phương Trình Bậc Nhất Một Ẩn !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lần lượt thay các giá trị của t vào hai vế của phương trình ta được:
- Tại t = -1 :
(t + 2)2 = (-1 + 2)2 = 1
3t + 4 = 3(-1) + 4 = 1
⇒ t = -1 là nghiệm của phương trình (t + 2)2 = 3t + 4.
- Tại t = 0
(t + 2)2 = (0 + 2)2 = 4
3t + 4 = 3.0 + 4 = 4
⇒ t = 0 là nghiệm của phương trình (t + 2)2 = 3t + 4.
- Tại t = 1
(t + 2)2 = (1 + 2)2 = 9
3t + 4 = 3.1 + 4 = 7
⇒ t = 1 không là nghiệm của phương trình (t + 2)2 = 3t + 4.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
- Phương trình x = 0 có tập nghiệm S1 = {0}.
- Xét phương trình x(x - 1) = 0. Vì một tích bằng 0 khi một trong hai thừa số bằng 0 tức là:
Nên phương trình này có tập nghiệm S2 = {0; 1}.
Vì S1 ≠ S2 nên hai phương trình không tương đương.
Lời giải
Vì phương trình nghiệm đúng với mọi x nên tập nghiệm của nó là S = R.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo