Cho tứ diện ABCD có AB = CD = 2. Gọi M, N lần lượt là trung điểm của AD, BC. Tính độ dài đoạn thẳng MN biết góc giữa hai đường thẳng AB và MN bằng 30° (làm tròn kết quả đến hàng phần trăm).
Cho tứ diện ABCD có AB = CD = 2. Gọi M, N lần lượt là trung điểm của AD, BC. Tính độ dài đoạn thẳng MN biết góc giữa hai đường thẳng AB và MN bằng 30° (làm tròn kết quả đến hàng phần trăm).
Quảng cáo
Trả lời:
Giải bởi Vietjack
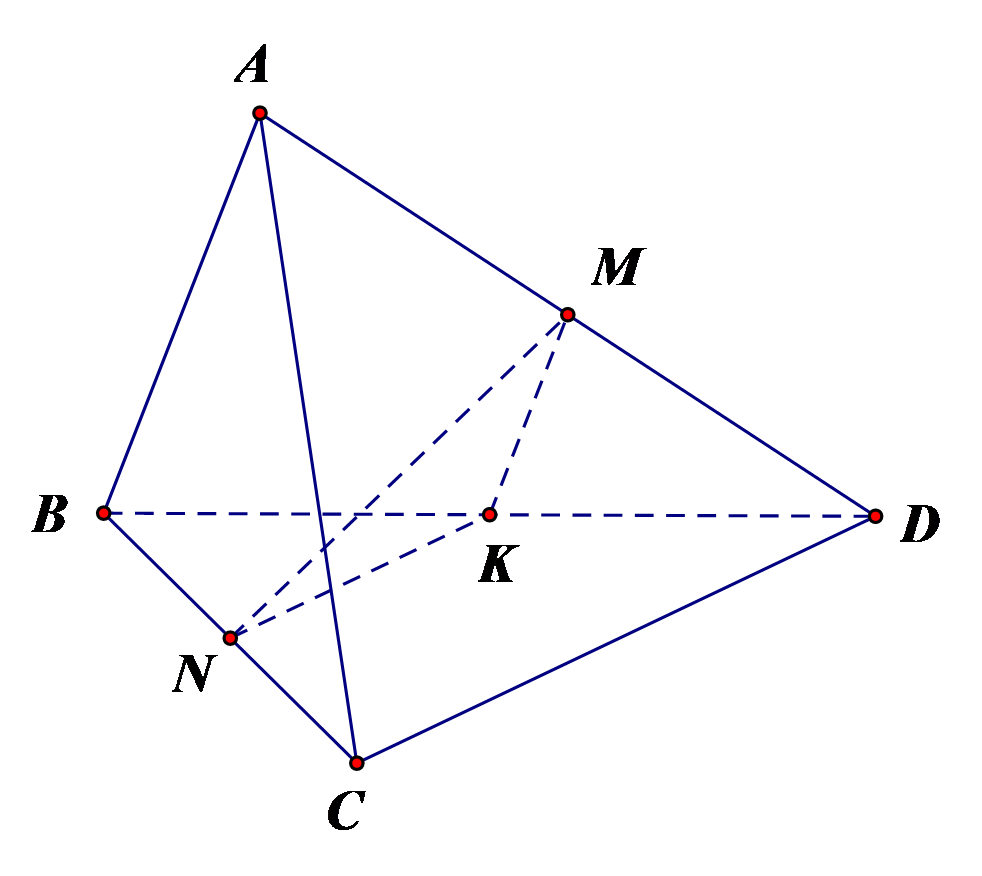
Gọi K là trung điểm của BD. Khi đó MK là đường trung bình của DABD.
Suy ra MK // AB; \(MK = \frac{{AB}}{2} = 1\).
Tương tự \(NK = \frac{{CD}}{2} = 1\).
Vì MK // AB nên (MN, AB) = (MN, MK) = \(\widehat {NMK} = 30^\circ \).
Xét DMNK có NK2 = MK2 + MN2 – 2MK.MN.cos30° Û 1 = 1 + MN2 – 2.1.MN.\(\frac{{\sqrt 3 }}{2}\)
Û \(M{N^2} - \sqrt 3 MN = 0 \Leftrightarrow MN = \sqrt 3 \approx 1,73\).
Trả lời: 1,73.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
D
Vì AC // A'C' nên (AM, A'C') = (AM, AC) = \(\widehat {MAC}\).
Vì DABC đều, AM là trung tuyến nên AM là phân giác của \(\widehat {BAC}\).
Do đó \(\widehat {MAC} = \frac{1}{2}\widehat {BAC} = 30^\circ \).
Câu 2
Cho hình hộp ABCD.A'B'C'D' có tất cả các cạnh đều bằng nhau. Trong các mệnh đề sau. mệnh đề nào sai?
A. BB' ^ BD.
B. A'C' ^ BD.
C. A'B ^ DC'.
D. BC' ^ A'D.
Lời giải
A
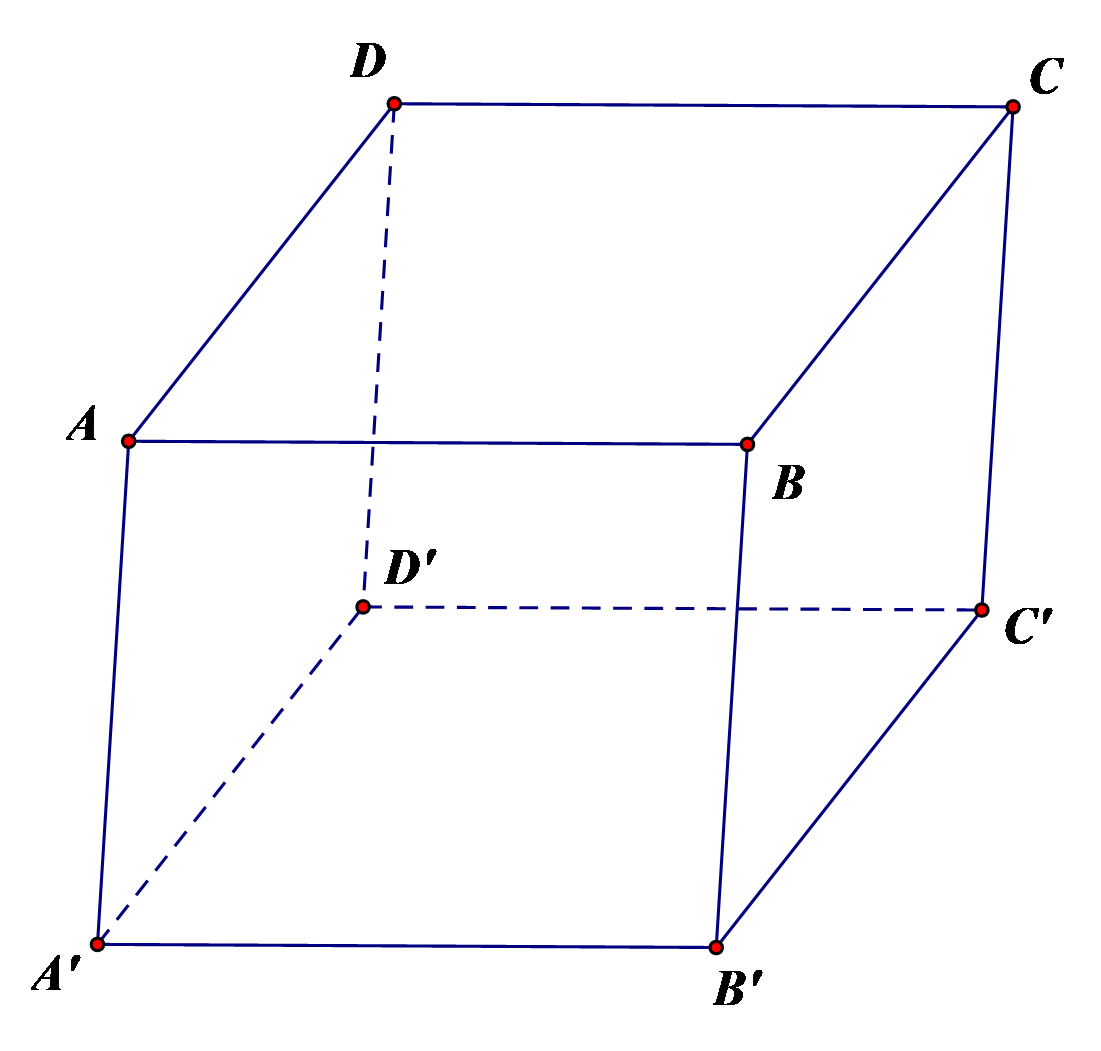
Do hình hộp ABCD.A'B'C'D' có tất cả các cạnh đều bằng nhau nên các mặt của hình hộp đều là hình thoi.
Suy ra A'C' ^ B'D' mà BD // B'D' nên A'C' ^ BD.
A'B ^ AB' mà AB' // DC' nên A'B ^ DC'.
BC' ^ B'C mà B'C // A'D nên BC' ^ A'D.
Câu 3
A. Nếu a và b cùng vuông góc với c thì a // b.
B. Nếu a // b và c ^ a thì c ^ b.
C. Nếu góc giữa a và c bằng góc giữa b và c thì a // b.
D. Nếu a và b cùng nằm trong mặt phẳng (α) // c thì góc giữa a và c bằng góc giữa b và c.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. 90°.
B. 45°.
C. 60°.
D. 30°.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập