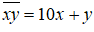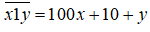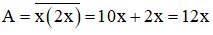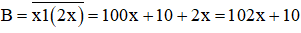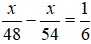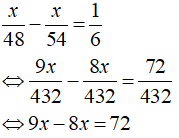Năm ngoái, tổng số dân của hai tỉnh A và B là 4 triệu. Năm nay, dân số của tỉnh A tăng thêm 1,1%, còn dân số của tỉnh B tăng thêm 1,2%. Tuy vậy số dân của tỉnh A năm nay vẫn nhiều hơn tỉnh B là 807200 người. Tính số dân năm ngoái của mỗi tỉnh.
Câu hỏi trong đề: Giải toán 8: Chương 3: Phương Trình Bậc Nhất Một Ẩn !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
* Phân tích:
| Năm ngoái | Năm nay | |
| Tỉnh A | x | x + x.1,1% = 1,011.x |
| Tỉnh B | 4 – x | (4 – x) + (4 – x).1,2% = (4 – x).1,012 |
Dân số tỉnh A năm nay nhiều hơn dân số tỉnh B là 807200 người = 0,8072 (triệu người) nên ta có phương trình:
1,011.x - 1,012.(4 – x) = 0,8072.
* Giải:
Gọi x là số dân năm ngoái của tỉnh A (0 < x < 4; x ∈ N*; triệu người)
Số dân năm ngoái của tỉnh B: 4 – x (triệu người).
Năm nay dân số của tỉnh A tăng 1,1 % nên số dân của tỉnh A năm nay: x + 1,1% x = 1,011.x
Năm nay dân số của tỉnh B tăng 1,2 % nên số dân của tỉnh B năm nay: (4 – x) + 1,2% (4 – x) = 1,012(4 – x)
Vì số dân tỉnh A năm nay hơn tỉnh B là 807200 người = 0,8072 triệu người nên ta có phương trình:
1,011.x - 1,012(4 – x) = 0,8072
⇔ 1,011x – 4,048 + 1,012x = 0,8072
⇔ 2,023. x = 4,8552
⇔ x = 2,4 (thỏa mãn).
Vậy dân số của tỉnh A năm ngoái là 2,4 triệu người, dân số tỉnh B năm ngoái là 4 – 2,4 = 1,6 triệu người
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
* Phân tích:
Với một số có hai chữ số bất kì ta luôn có: 
Khi thêm chữ số 1 xen vào giữa ta được số: 
Vì chữ số hàng đơn vị gấp 2 lần chữ số hàng chục nên ta có y = 2x.
Số mới lớn hơn số ban đầu 370 nên ta có phương trình:
100x + 10 + 2x = 10x + 2x + 370.
* Giải:
Gọi chữ số hàng chục của số cần tìm là x (x ∈ N; 0 < x ≤ 9).
⇒ Chữ số hàng đơn vị là 2x
⇒ Số cần tìm bằng 
Sau khi viết thêm chữ số 1 vào giữa hai chữ số ta được số mới là:
Theo đề bài số mới lớn hơn số ban đầu 370, ta có B = A + 370 nên ta có phương trình
102x + 10 = 12x + 370
⇔ 102x – 12x = 370 – 10
⇔ 90x = 360
⇔ x = 4 (thỏa mãn)
Vậy số cần tìm là 48.
*Lưu ý : Vì chỉ có 4 số có hai chữ số thỏa mãn điều kiện chữ số hàng đơn vị gấp đôi chữ số hàng chục là : 12 ; 24 ; 36 ; 48 nên ta có thể đi thử trực tiếp mà không cần giải bằng cách lập phương trình.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
* Phân tích:
Ta luôn có: Quãng đường = vận tốc . thời gian
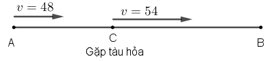
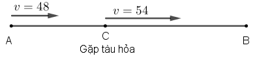
Gọi C là địa điểm ô tô gặp tàu hỏa.
Quãng đường AC ô tô đi với vận tốc 48km/h trong 1h nên SAC = 48km.
Xét trên quãng đường BC, để đến B đúng thời gian đã định ô tô đi với vận tốc 48 + 6 = 54 (km/h).
Vì ô tô đến B đúng thời gian đã định nên thời gian thực tế ô tô đi từ B đến C ít hơn thời gian dự định là 10 phút = 1/6 giờ (là thời gian chờ tàu hỏa).
| Quãng đường BC | Vận tốc | Thời gian | |
| Dự tính | x | 48 |  |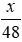
| Thực tế | x | 48 + 6 = 54 |  |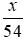
Ta có phương trình: 
* Giải:
Gọi C là địa điểm ô tô gặp tàu hỏa.
Quãng đường AC ô tô đi với vận tốc 48km/h và đi trong 1 giờ
⇒ SAC = 48.1 = 48 (km).
Gọi quãng đường BC dài là x (km; x > 0).
Vận tốc dự tính đi trên BC là: 48 km/h
⇒ Thời gian dự tính đi quãng đường BC hết: 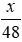(giờ).
Thực tế ô tô đi quãng đường BC với vận tốc bằng 48 + 6 = 54 (km/h).
⇒ Thời gian thực tế ô tô đi quãng đường BC là: 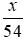(giờ).
Thời gian chênh nhau giữa dự tính và thực tế chính là thời gian ô tô đợi tàu hỏa là 10 phút = 1/6 (giờ).
Do đó ta có phương trình:
⇔ x = 72 (thỏa mãn) nên quãng đường BC là 72 (km).
Vậy quãng đường AB là:
SAB = SAC + SBC = 48 + 72 = 120 (km).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập